题目内容
20．复数$\frac{-i}{1-2i}（i$是虚数单位）的共轭复数为（ ）| A． | $-\frac{2}{5}+\frac{i}{5}$ | B． | $-\frac{2}{5}-\frac{i}{5}$ | C． | $\frac{2}{5}-\frac{i}{5}$ | D． | $\frac{2}{5}+\frac{i}{5}$ |
分析 直接由复数代数形式的乘除运算化简复数$\frac{-i}{1-2i}$，则复数$\frac{-i}{1-2i}（i$是虚数单位）的共轭复数可求．
解答 解：∵$\frac{-i}{1-2i}=\frac{-i（1+2i）}{（1-2i）（1+2i）}=\frac{2-i}{5}=\frac{2}{5}-\frac{1}{5}i$，
∴复数$\frac{-i}{1-2i}（i$是虚数单位）的共轭复数为：$\frac{2}{5}+\frac{1}{5}i$．
故选：D．
点评 本题考查了复数代数形式的乘除运算，考查了复数的基本概念，是基础题．
练习册系列答案
相关题目
8．已知函数f（x）=（x2+ax+b）ex，当b＜1时，函数f（x）在（-∞，-2），（1，+∞）上均为增函数，则$\frac{a+b}{a-2}$的取值范围是（ ）
| A． | （-2，$\frac{2}{3}$] | B． | [-$\frac{1}{3}$，2） | C． | （-∞，$\frac{2}{3}$] | D． | [-$\frac{2}{3}$，2] |
15．已知复数z满足z•i=1+i（i是虚数单位），则复数z的共轭复数在复平面内所对应的点的坐标为（ ）
| A． | （1，1） | B． | （-1，-1） | C． | （1，-1） | D． | （-1，1） |
5．
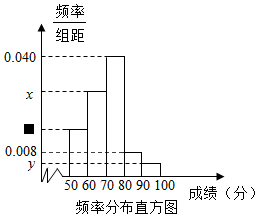某中学为了解某次竞赛成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100分）作为样本进行统计，请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图解决下列问题：
频率分布表：
（1）写出a，b，x，y的值；
（2）在选取的样本中，从竞赛成绩是80分以上（含80分）的同学中随机抽取2名同学参加座谈，求所抽取的2名同学来自同一组的概率．
某中学为了解某次竞赛成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100分）作为样本进行统计，请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图解决下列问题：频率分布表：
| 组别 | 分组 | 频数 | 频率 |
| 第1组 | [50，60） | 9 | 0.18 |
| 第2组 | [60，70） | a | ▓ |
| 第3组 | [70，80） | 20 | 0.40 |
| 第4组 | [80，90） | ▓ | 0.08 |
| 第5组 | [90，100] | 2 | b |
| 合计 | ▓ | ▓ |
（2）在选取的样本中，从竞赛成绩是80分以上（含80分）的同学中随机抽取2名同学参加座谈，求所抽取的2名同学来自同一组的概率．
若正整数N除以正整数m后的余数为n，则记为N≡n（mod m），例如10≡4（mod 6）．下面程序框图的算法源于我国古代闻名中外的（中国剩余定理），执行该程序框图，则输出的n等于（ ）