题目内容
13．设A是非空数集，0∉A，1∉A，且满足条件：若x∈A，则$\frac{1}{1-x}$∈A．若2∈A，则集合A中所含元素个数最小的集合A{2，-1，$\frac{1}{2}$}．分析 利用x∈A，则$\frac{1}{1-x}$∈A．即可得出．
解答 解：∵2∈A，∴$\frac{1}{1-2}$=-1∈A，
∴$\frac{1}{1-（-1）}$=$\frac{1}{2}∈$A，
∴$\frac{1}{1-\frac{1}{2}}$=2∈A，
因此A={2，-1，$\frac{1}{2}$}．
故答案为：{2，-1，$\frac{1}{2}$}．
点评 本题考查了元素与集合之间的关系、方程的解法，考查了推理能力与计算能力，属于基础题．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
18．已知a，b为实数，则“a3＜b3”是“2a＜2b”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分又不必要条件 |
4．已知F1，F2分别是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左右两个焦点，若在双曲线C上存在点P使∠F1PF2=90°，且满足2∠PF1F2=∠PF2F1，那么双曲线C的离心率为（ ）
| A． | $\sqrt{3}$+1 | B． | 2 | C． | $\sqrt{3}$ | D． | $\frac{\sqrt{5}}{2}$ |
5．
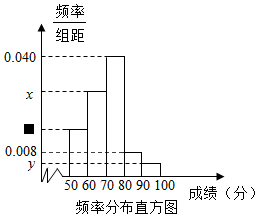某中学为了解某次竞赛成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100分）作为样本进行统计，请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图解决下列问题：
频率分布表：
（1）写出a，b，x，y的值；
（2）在选取的样本中，从竞赛成绩是80分以上（含80分）的同学中随机抽取2名同学参加座谈，求所抽取的2名同学来自同一组的概率．
某中学为了解某次竞赛成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100分）作为样本进行统计，请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图解决下列问题：频率分布表：
| 组别 | 分组 | 频数 | 频率 |
| 第1组 | [50，60） | 9 | 0.18 |
| 第2组 | [60，70） | a | ▓ |
| 第3组 | [70，80） | 20 | 0.40 |
| 第4组 | [80，90） | ▓ | 0.08 |
| 第5组 | [90，100] | 2 | b |
| 合计 | ▓ | ▓ |
（2）在选取的样本中，从竞赛成绩是80分以上（含80分）的同学中随机抽取2名同学参加座谈，求所抽取的2名同学来自同一组的概率．