题目内容
10.设α为第二象限,若sinα+cosα=-$\frac{\sqrt{10}}{5}$,则tan(α+$\frac{π}{4}$)等于( )| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |
分析 由条件利用同角三角函数的基本关系,以及三角函数在各个象限中的符号,求得sin(α+$\frac{π}{4}$)和cos(α+$\frac{π}{4}$)的值,可得tan(α+$\frac{π}{4}$)的值.
解答 解:∵α为第二象限,若sinα+cosα=$\sqrt{2}$sin(α+$\frac{π}{4}$)=-$\frac{\sqrt{10}}{5}$,
∴sin(α+$\frac{π}{4}$)=-$\frac{\sqrt{5}}{5}$<0,∴α+$\frac{π}{4}$为第三象限角,cos(α+$\frac{π}{4}$)<0.
再根据${sin}^{2}(α+\frac{π}{4})$+${cos}^{2}(α+\frac{π}{4})$=1,求得cos(α+$\frac{π}{4}$)=-$\frac{2\sqrt{5}}{5}$,
则tan(α+$\frac{π}{4}$)=$\frac{sin(α+\frac{π}{4})}{cos(α+\frac{π}{4})}$=$\frac{1}{2}$,
故选:B.
点评 本题主要考查同角三角函数的基本关系,以及三角函数在各个象限中的符号,属于基础题.

练习册系列答案
相关题目
18.已知a,b为实数,则“a3<b3”是“2a<2b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
18.运行如图所示的程序框图,则输出的结果是( )
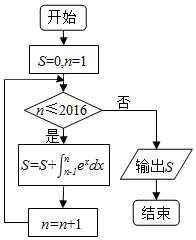

| A. | e2016-e2015 | B. | e2017-e2016 | C. | e2015-1 | D. | e2016-1 |
5.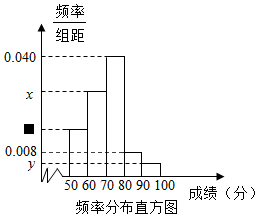 某中学为了解某次竞赛成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图解决下列问题:
某中学为了解某次竞赛成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图解决下列问题:
频率分布表:
(1)写出a,b,x,y的值;
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学参加座谈,求所抽取的2名同学来自同一组的概率.
 某中学为了解某次竞赛成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图解决下列问题:
某中学为了解某次竞赛成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图解决下列问题:频率分布表:
| 组别 | 分组 | 频数 | 频率 |
| 第1组 | [50,60) | 9 | 0.18 |
| 第2组 | [60,70) | a | ▓ |
| 第3组 | [70,80) | 20 | 0.40 |
| 第4组 | [80,90) | ▓ | 0.08 |
| 第5组 | [90,100] | 2 | b |
| 合计 | ▓ | ▓ |
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学参加座谈,求所抽取的2名同学来自同一组的概率.
15.下列命题错误的是( )
| A. | “a>b”是“log2a>log2b”的必要不充分条件 | |
| B. | 命题p:?n∈N,n2>2n,则¬p:?x∈N,n2≤2n | |
| C. | 函数f(x)=x-sinx既是奇函数又是增函数 | |
| D. | 方程Ax2+By2=1表示椭圆的充要条件是A>O,B>0 |
19.两组学校的社会实践活动各有7位人员(下文分别简称为“甲小组”和“乙小组”).两小组成员分别独立完成一项社会调查,并形成调查报告,每位成员从启动调查到完成报告所用的时间(单位:天)如表所示:
假设所有成员所用时间相互了独立,从甲、乙两小组随机各选1人,甲小组选出的人记为A,乙小组选出的人记为B.
(Ⅰ)求A所用时间不小于13天的概率;
(Ⅱ)如果a=18,求A所用的时间比B所用时间长的概率.
| 组别 | 每位成员从启动调查到完成报告所用的时间(单位:天) | ||||||
| 甲小组 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 乙小组 | 12 | 13 | 15 | 16 | 17 | 14 | a |
(Ⅰ)求A所用时间不小于13天的概率;
(Ⅱ)如果a=18,求A所用的时间比B所用时间长的概率.
20.i为虚数单位,则复数$\frac{1-2i}{i}$的共轭复数是( )
| A. | -1+2i | B. | 1-2i | C. | -2+i | D. | 2-i |
