题目内容
15.已知复数z满足$z=\frac{a+i}{2-i}+a$为纯虚数,则复数|z|的模为( )| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{3}{7}$ | D. | $\frac{1}{3}$ |
分析 利用复数的运算法则、纯虚数的定义、模的计算公式即可得出.
解答 解:$z=\frac{(a+i)(2+i)}{5}+a=\frac{(7a-1)+(a+2)i}{5}$,为纯虚数,
∴$\frac{7a-1}{5}$=0,$\frac{a+2}{5}$≠0,解得$a=\frac{1}{7}$,
∴z=$\frac{3}{7}$i.
∴$|z|=\frac{3}{7}$.
故选:C.
点评 本题考查了复数的运算法则、纯虚数的定义、模的计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
6.设P为双曲线${x^2}-\frac{y^2}{15}=1$右支上一点,M,N分别是圆(x+4)2+y2=4和(x-4)2+y2=1上的点,设|PM|-|PN|的最大值和最小值分别为m,n,则|m-n|=( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
13.观察数列1,2,2,3,3,3,8,8,8,…的特点,按此规律,则第100项为( )
| A. | 213 | B. | 214 | C. | 215 | D. | 216 |
14.将一个大正方形平均分成9个小正方形,向大正方形区域随机投掷一个点(每次都能投中),投中最左侧三个小正方形区域的事件记为A,投中最上面三个小正方形区域或正中间的一个小正方形区域的事件记为B,则P(A|B)=( )
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{9}$ |
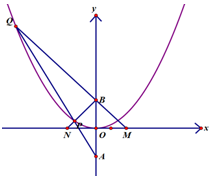 已知抛物线的方程为x2=2py(p>0),过点A(0,-a)(a>0)作直线l与抛物线相交于P,Q两点,点B的坐标为(0,a),连接BP,BQ.且QB,QP与x轴分别交于M,N两点,如果QB的斜率与PB的斜率之积为-3,则∠PBQ=$\frac{2π}{3}$.
已知抛物线的方程为x2=2py(p>0),过点A(0,-a)(a>0)作直线l与抛物线相交于P,Q两点,点B的坐标为(0,a),连接BP,BQ.且QB,QP与x轴分别交于M,N两点,如果QB的斜率与PB的斜率之积为-3,则∠PBQ=$\frac{2π}{3}$.