题目内容
6.设P为双曲线${x^2}-\frac{y^2}{15}=1$右支上一点,M,N分别是圆(x+4)2+y2=4和(x-4)2+y2=1上的点,设|PM|-|PN|的最大值和最小值分别为m,n,则|m-n|=( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 求得两圆的圆心和半径,设双曲线的左右焦点为F1(-4,0),F2(4,0),连接PF1,PF2,F1M,F2N,运用勾股定理和双曲线的定义,结合三点共线时,距离之和取得最小值,计算即可得到所求值.
解答  解:圆C1:(x+4)2+y2=4的圆心为(-4,0),半径为r1=2;
解:圆C1:(x+4)2+y2=4的圆心为(-4,0),半径为r1=2;
圆C2:(x-4)2+y2=1的圆心为(4,0),半径为r2=1,
设双曲线${x^2}-\frac{y^2}{15}=1$的左右焦点为F1(-4,0),F2(4,0),
连接PF1,PF2,F1M,F2N,可得|PF1|-|PF2|=2是定值,|PM|=|PF1|+r1,
|PN|=(|PF2|-r2),所以|PM|-|PN|的最大值2a+r1+r2=5,
|PM|=|PF1|-r1,
|PN|=(|PF2|+r2),所以|PM|-|PN|的最小值:2a-r1-r2=-1.
可得m=5,n=-1,则|m-n|=6.
故选:C.
点评 本题考查最值的求法,注意运用双曲线的定义和圆的方程,考查三点共线的性质,以及运算能力,属于中档题.

练习册系列答案
相关题目
16.过抛物线C:y2=2px(p>0)焦点F的直线l与C相交于A,B两点,与C的准线交于点D,若|AB|=|BD|,则直线l的斜率k=( )
| A. | $±\frac{1}{3}$ | B. | ±3 | C. | $±\frac{{2\sqrt{2}}}{3}$ | D. | $±2\sqrt{2}$ |
17.已知(3+2i)x=2-yi,其中 x,y是实数,则|x+yi|=( )
| A. | 2 | B. | $\frac{{2\sqrt{5}}}{3}$ | C. | $\frac{{\sqrt{10}}}{3}$ | D. | $\frac{1}{3}$ |
14.已知函数f(x)=2x+sinx,不等式f(m2)+f(2m-3)<0(其中m∈R)的解集是( )
| A. | (-3,1) | B. | (-1,3) | C. | (-∞,-3)∪(1,+∞) | D. | (-∞,-1)∪(3,+∞) |
18.a2+b2=1是asinθ+bcosθ≤1恒成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.已知复数z满足$z=\frac{a+i}{2-i}+a$为纯虚数,则复数|z|的模为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{3}{7}$ | D. | $\frac{1}{3}$ |
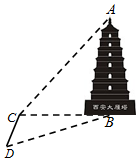 如图,某数学兴趣小组为了测量西安大雁塔高AB,选取与塔底B在同一水平面
如图,某数学兴趣小组为了测量西安大雁塔高AB,选取与塔底B在同一水平面 在△ABC中,D、E分别是AB、AC的中点,M是直线DE上的动点.若△ABC的面积为2,则$\overrightarrow{MB}$•$\overrightarrow{MC}$+$\overrightarrow{BC}$2的最小值为2$\sqrt{3}$.
在△ABC中,D、E分别是AB、AC的中点,M是直线DE上的动点.若△ABC的面积为2,则$\overrightarrow{MB}$•$\overrightarrow{MC}$+$\overrightarrow{BC}$2的最小值为2$\sqrt{3}$.