题目内容
10.函数f(x)=$\sqrt{-x}+\sqrt{x(x+1)}$的定义域为{x|x≤-1或x=0}.分析 直接由根式内部的代数式大于等于0联立不等式组求解.
解答 解:由$\left\{\begin{array}{l}{-x≥0}\\{x(x+1)≥0}\end{array}\right.$,解得x≤-1或x=0.
∴函数f(x)=$\sqrt{-x}+\sqrt{x(x+1)}$的定义域为:{x|x≤-1或x=0}.
故答案为:{x|x≤-1或x=0}.
点评 本题考查函数的定义域及其求法,是基础的计算题.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
18.a2+b2=1是asinθ+bcosθ≤1恒成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.已知复数z满足$z=\frac{a+i}{2-i}+a$为纯虚数,则复数|z|的模为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{3}{7}$ | D. | $\frac{1}{3}$ |
2.某投资公司现提供两种一年期投资理财方案,一年后投资盈亏的情况如表:
( I)甲、乙两人在投资顾问的建议下分别选择“投资股市”和“购买基金”,若一年后他们中至少有一人盈利的概率大于$\frac{4}{5}$,求p的取值范围;
( II)某人现有10万元资金,决定在“投资股市”和“购买基金”这两种方案中选出一种,若购买基金现阶段分析出$p=\frac{1}{2}$,那么选择何种方案可使得一年后的投资收益的数学期望值较大?
| 投资股市 | 获利40% | 不赔不赚 | 亏损20% | 购买基金 | 获利20% | 不赔不赚 | 亏损10% |
| 概率P | $\frac{1}{2}$ | $\frac{1}{8}$ | $\frac{3}{8}$ | 概率P | p | $\frac{1}{3}$ | q |
( II)某人现有10万元资金,决定在“投资股市”和“购买基金”这两种方案中选出一种,若购买基金现阶段分析出$p=\frac{1}{2}$,那么选择何种方案可使得一年后的投资收益的数学期望值较大?
8.若集合A={x|x2+2x-8<0},集合B={x|-2<x<4},则A∩B等于( )
| A. | ∅ | B. | (-2,3) | C. | (-2,4) | D. | (-2,2) |
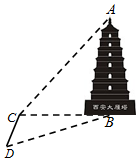 如图,某数学兴趣小组为了测量西安大雁塔高AB,选取与塔底B在同一水平面
如图,某数学兴趣小组为了测量西安大雁塔高AB,选取与塔底B在同一水平面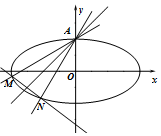 如图,已知直线l:y=kx+1(k>0)关于直线y=x+1对称的直线为l1,直线l,l1与椭圆E:$\frac{x^2}{4}+{y^2}$=1分别交于点A、M和A、N,记直线l1的斜率为k1.
如图,已知直线l:y=kx+1(k>0)关于直线y=x+1对称的直线为l1,直线l,l1与椭圆E:$\frac{x^2}{4}+{y^2}$=1分别交于点A、M和A、N,记直线l1的斜率为k1.