题目内容
19.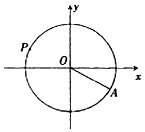 水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然和改造自然的象征.如图是一个半径为R的水车,一个水斗从点A(3$\sqrt{3}$,-3)出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时60秒.经过t秒后,水斗旋转到P点,设P的坐标为(x,y),其纵坐标满足y=f(t)=Rsin(ωt+φ)(t≥0,ω>0,|φ|<$\frac{π}{2}}$).则下列叙述错误的是( )
水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然和改造自然的象征.如图是一个半径为R的水车,一个水斗从点A(3$\sqrt{3}$,-3)出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时60秒.经过t秒后,水斗旋转到P点,设P的坐标为(x,y),其纵坐标满足y=f(t)=Rsin(ωt+φ)(t≥0,ω>0,|φ|<$\frac{π}{2}}$).则下列叙述错误的是( )| A. | $R=6,ω=\frac{π}{30},φ=-\frac{π}{6}$ | |
| B. | 当t∈[35,55]时,点P到x轴的距离的最大值为6 | |
| C. | 当t∈[10,25]时,函数y=f(t)单调递减 | |
| D. | 当t=20时,$|{PA}|=6\sqrt{3}$ |
分析 求出函数的解析式,再分析选项,即可得出结论.
解答 解:由题意,R=$\sqrt{27+9}$=6,T=60=$\frac{2π}{ω}$,∴ω=$\frac{π}{30}$,
点A(3$\sqrt{3}$,-3)代入可得-3=6sinφ,∵|φ|<$\frac{π}{2}}$),∴φ=-$\frac{π}{6}$.故A正确;
f(t)=6sin($\frac{π}{30}$t-$\frac{π}{6}$),当t∈[35,55]时,$\frac{π}{30}$t-$\frac{π}{6}$∈[π,$\frac{5}{3}π$],∴点P到x轴的距离的最大值为6,正确;
当t∈[10,25]时,$\frac{π}{30}$t-$\frac{π}{6}$∈[$\frac{1}{6}$π,$\frac{2π}{3}$],函数y=f(t)单调递减,不正确;
当t=20时,$\frac{π}{30}$t-$\frac{π}{6}$=$\frac{π}{2}$,P的纵坐标为6,|PA|=$\sqrt{27+81}$=6$\sqrt{3}$,正确,
故选C.
点评 本题主要考查了在实际问题中建立三角函数模型的问题.考查了运用三角函数的最值,周期等问题确定函数的解析式.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
10.“共享单车”的出现,为我们提供了一种新型的交通方式.某机构为了调查人们对此种交通方式的满意度,从交通拥堵不严重的A城市和交通拥堵严重的B城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如图:
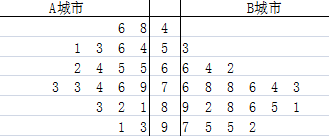
(Ⅰ)根据茎叶图,比较两城市满意度评分的平均值和方差(不要求计算出具体值,得出结论即可);
(Ⅱ)若得分不低于80分,则认为该用户对此种交通方式“认可”,否则认为该用户对此种交通方式“不认可”,请根据此样本完成下列2×2列联表,并据此样本分析你是否有95%的把握认为城市拥堵与认可共享单车有关.
(参考公式:${Χ^2}=\frac{{n{{({n_{11}}{n_{22}}-{n_{12}}{n_{21}})}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}$)
(Ⅲ)在A和B两个城市满意度在90分以上的用户中任取2户,求来自不同城市的概率.

(Ⅰ)根据茎叶图,比较两城市满意度评分的平均值和方差(不要求计算出具体值,得出结论即可);
(Ⅱ)若得分不低于80分,则认为该用户对此种交通方式“认可”,否则认为该用户对此种交通方式“不认可”,请根据此样本完成下列2×2列联表,并据此样本分析你是否有95%的把握认为城市拥堵与认可共享单车有关.
| 认可 | 不认可 | 合计 | |
| A城市 | |||
| B城市 | |||
| 合计 |
| P(Χ2≥k) | 0.05 | 0.010 |
| k | 3.841 | 6.635 |
(Ⅲ)在A和B两个城市满意度在90分以上的用户中任取2户,求来自不同城市的概率.
7.已知命题p1:若sinx≠0,则sinx+$\frac{1}{sinx}$≥2恒成立;p2:x+y=0的充要条件是$\frac{x}{y}$=-1,则下列命题为真命题的是( )
| A. | p1∧p2 | B. | p1∨p2 | C. | p1∧(¬p2) | D. | (¬p1)∨p2 |
14.已知角α的顶点与坐标原点重合,始边与x轴的非负半轴重合,终边经过点P(1,-2),则sin2α=( )
| A. | $-\frac{4}{5}$ | B. | $-\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
5.函数y=2xex的一个原函数为( )
| A. | 2xex(1+ln2) | B. | $\frac{{2}^{x}{e}^{x}}{(1+ln2)}$ | C. | 2exln2 | D. | $\frac{2{e}^{x}}{ln2}$ |
2.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点分别为F1、F2,P为双曲线右支上一点,且$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0$,若$∠P{F_1}{F_2}∈[{\frac{π}{12},\frac{π}{6}}]$,则双曲线离心率的取值范围是( )
| A. | $[{2,\sqrt{3}+1}]$ | B. | $[{2,2\sqrt{3}+1}]$ | C. | $[{\sqrt{2},2}]$ | D. | $[{\sqrt{2},\sqrt{3}+1}]$ |