题目内容
某耗水量较大的企业为积极响应政府号召,对生产设备进行技术改造,以达到节约用水的目的.下表提供了该企业节约用水技术改造后生产某产品过程中记录的产量x(吨)与相应的生产用水y(吨)的几组对照数据:
(1)请根据表中提供的数据,计算
和
的值,已知x,y之间呈线性相关关系,求y关于x的线性回归方程
=
x+
,并解释
的含义;
(参考数据:
xi2=54,
xiyi=65.3)
(2)已知该厂技术改造前100吨该产品的生产用水为130吨,试根据(1)中求出的线性回归方程,预测技术改造后生产100吨该产品的用水量比技术改造前减少了多少吨?
| x | 2 | 3 | 4 | 5 |
| y | 3 | 3.5 | 4.7 | 6 |
. |
| x |
. |
| y |
 |
| y |
 |
| b |
 |
| a |
 |
| b |
(参考数据:
| 4 |
 |
| i=1 |
| 4 |
 |
| i=1 |
(2)已知该厂技术改造前100吨该产品的生产用水为130吨,试根据(1)中求出的线性回归方程,预测技术改造后生产100吨该产品的用水量比技术改造前减少了多少吨?
考点:线性回归方程
专题:概率与统计
分析:(1)根据所给的这组数据求出利用最小二乘法所需要的几个数据,代入求系数b的公式,求得结果,再把样本中心点代入,求出a的值,得到线性回归方程.
(2)根据上一问所求的线性回归方程,把x=100代入线性回归方程,预测生产100吨甲产品的用水量比技术改造前的数量.
(2)根据上一问所求的线性回归方程,把x=100代入线性回归方程,预测生产100吨甲产品的用水量比技术改造前的数量.
解答:
解:(1)由对照数据,由题意可知:
xi2=54,
xiyi=65.3
=
=3.5,
=
(3+3.5+4.7+6)=4.3,…(2分)
所以,由最小二乘法确定的回归方程的系数为:
=
=1.02,
=4.3-1.02×3.5=0.73.…(5分)
所求的线性回归方程为
=1.02x+0.73…(8分)
(2)由(1)的回归方程及技改前生产100吨甲产品的生产用水,得减少的生产用水量为130-(1.02×100+0.73)=27.27(吨水)…(12分)
| 4 |
 |
| i=1 |
| 4 |
 |
| i=1 |
. |
| x |
| 2+3+4+5 |
| 4 |
. |
| y |
| 1 |
| 4 |
所以,由最小二乘法确定的回归方程的系数为:
 |
| b |
| 65.3-4×3.5×4.3 |
| 54-4×3.52 |
| ? |
| a |
所求的线性回归方程为
| ? |
| y |
(2)由(1)的回归方程及技改前生产100吨甲产品的生产用水,得减少的生产用水量为130-(1.02×100+0.73)=27.27(吨水)…(12分)
点评:本题考查线性回归方程的求法,考查最小二乘法,是一个基础题,解题时运算量比较大,注意利用公式求系数时,不要在运算上出错.属于中档题.

练习册系列答案
相关题目
求f(x)=
的定义域( )
| log2(-x2-5x+6) |
| x+2 |
| A、(-6,1) |
| B、(-∞,-6)∪(1,+∞) |
| C、(-6,-2)∪(-2,1) |
| D、R |
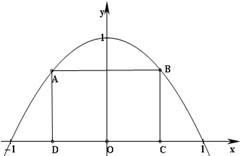 如图所示,抛物线y=1-x2与x轴所围成的区域是一块等待开垦的土地,现计划在该区域内围出一块矩形地块ABCD作为工业用地,其中A、B在抛物线上,C、D在x轴上.已知工业用地每单位面积价值为3a元(a>0),其它的三个边角地块每单位面积价值a元.
如图所示,抛物线y=1-x2与x轴所围成的区域是一块等待开垦的土地,现计划在该区域内围出一块矩形地块ABCD作为工业用地,其中A、B在抛物线上,C、D在x轴上.已知工业用地每单位面积价值为3a元(a>0),其它的三个边角地块每单位面积价值a元.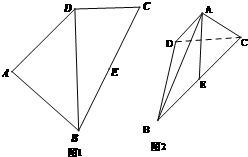 如图,四边形ABCD中(图1),E是BC的中点,DB=2,DC=1,BC=
如图,四边形ABCD中(图1),E是BC的中点,DB=2,DC=1,BC=