题目内容
沿对角线AC将正方形ABCD折成直二面角后，AB与CD所在的直线所成的角等于 ．
考点：异面直线及其所成的角
专题：空间角
分析：取AC、BD、BC的中点依次为E、F、G，连接BD、EF、EG、FG，则FG∥CD，EG∥AB，∠FGE为异面直线AB与CD所成的角，由此能求出结果．
解答：
解：如下图，取AC、BD、BC的中点依次为E、F、G，
连接BD、EF、EG、FG，
则FG∥CD，EG∥AB，
故∠FGE为异面直线AB与CD所成的角（或其补角），
设正方形的边长为2个单位，则FG=1，EG=1，EF=1，
从而∠FGE=60°，
故答案为：60°．
连接BD、EF、EG、FG，
则FG∥CD，EG∥AB，
故∠FGE为异面直线AB与CD所成的角（或其补角），
设正方形的边长为2个单位，则FG=1，EG=1，EF=1，
从而∠FGE=60°，
故答案为：60°．
点评：本题考查异面直线所成角的求法，是基础题，解题时要认真审题，注意空间思维培养．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
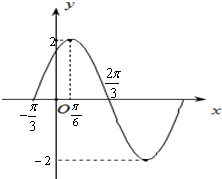已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的部分图象如图所示．