题目内容
已知a和b是任意非零实数.
(1)求
的最小值.
(2)若不等式|2a+b|+|2a-b|≥|a|(|2+x|+|2-x|)恒成立,求实数x的取值范围.
(1)求
| |2a+b|+|2a-b| |
| |a| |
(2)若不等式|2a+b|+|2a-b|≥|a|(|2+x|+|2-x|)恒成立,求实数x的取值范围.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(1)由条件利用绝对值三角不等式求得
的最小值.
(2)由条件利用绝对值三角不等式|2+x|+|2-x|≤4,再根据绝对值的意义可得|2+x|+|2-x|≥4,从而得到|2+x|+|2-x|=4,由此利用绝对值的意义求得x的范围.
| |2a+b|+|2a-b| |
| |a| |
(2)由条件利用绝对值三角不等式|2+x|+|2-x|≤4,再根据绝对值的意义可得|2+x|+|2-x|≥4,从而得到|2+x|+|2-x|=4,由此利用绝对值的意义求得x的范围.
解答:
解:(1)∵
=|
|+|
|=|2+
|+|2-
|≥|(2+
)+(2-
)|=4,
所以
的最小值为4.
(2)∵|2a+b|+|2a-b|≥|2a+b+2a-b|=4|a|,不等式|a+b|+|a-b|≥|a|(|2+x|+|2-x|)恒成立,
∴4|a||≥|a|(|2+x|+|2-x|),即|2+x|+|2-x|≤4.
而|2+x|+|2-x|表示数轴上的x对应点到-2、2对应点的距离之和,它的最小值为4,
故|2+x|+|2-x|=4,∴-2≤x≤2,
即实数x的取值范围为:[-2,2].
| |2a+b|+|2a-b| |
| |a| |
| 2a+b |
| a |
| 2a-b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
所以
| |2a+b|+|2a-b| |
| |a| |
(2)∵|2a+b|+|2a-b|≥|2a+b+2a-b|=4|a|,不等式|a+b|+|a-b|≥|a|(|2+x|+|2-x|)恒成立,
∴4|a||≥|a|(|2+x|+|2-x|),即|2+x|+|2-x|≤4.
而|2+x|+|2-x|表示数轴上的x对应点到-2、2对应点的距离之和,它的最小值为4,
故|2+x|+|2-x|=4,∴-2≤x≤2,
即实数x的取值范围为:[-2,2].
点评:本题主要考查绝对值的意义,绝对值不等式的解法,绝对值三角不等式,函数的恒成立问题,体现了等价转化的数学思想,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=
(sint-lgt)dt(x>1),则f(x)的极大值点的个数为( )
| ∫ | x 1 |
| A、0 | B、1 | C、2 | D、3 |


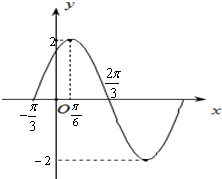 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示.