题目内容
设a，b，c均为正数，且x=a+
，y=b+
，z=c+
，则x，y，z三个数（ ）
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
| A、至少有一个不大于2 |
| B、都小于2 |
| C、至少有一个不小于2 |
| D、都大于2 |
考点：基本不等式
专题：不等式的解法及应用
分析：本题可以先猜想出相关结论，再用反证法加以证明．
解答：
解：（反证法）
假设x，y，z三个数均小于2，即x＜2，y＜2，z＜2．
则x+y+z＜6 ①
又∵x+y+z=a+
+b+
+c+
=(a+
)+(b+
)+(c+
)
≥2
+2
+2
=6．
即x+y+z≥6 ②
∴①②矛盾，假设不成立．
∴x，y，z三个数至少有一个不小于2．
故选C．
假设x，y，z三个数均小于2，即x＜2，y＜2，z＜2．
则x+y+z＜6 ①
又∵x+y+z=a+
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
=(a+
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
≥2
a•
|
b•
|
c•
|
=6．
即x+y+z≥6 ②
∴①②矛盾，假设不成立．
∴x，y，z三个数至少有一个不小于2．
故选C．
点评：本题考查的知识点是反证法、基本不等式，思维难度不大，运算量适中，属于中档题．
练习册系列答案
相关题目
设非零向量
，
，
，满足|
+
|=|
-
|，且|
|=|
|=|
+
+
|=1，则|
|的取值范围是（ ）
| x |
| y |
| z |
| x |
| y |
| x |
| y |
| x |
| y |
| x |
| y |
| z |
| ||||
|
|
| A、[0，2] | ||||||||
B、[1-
| ||||||||
C、[0，
| ||||||||
| D、[1，2] |
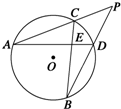如图所示，⊙O的两条弦AD和CB相交于点E，AC和BD的延长线相交于点P，下面结论：①PA•PC=PD•PB；
②PC•CA=PB•BD；
③CE•CD=BE•BA；
④PA•CD=PD•AB．
其中正确的有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
若（9x-
）n（n∈N*）的展开式的第3项的二项式系数为36，则其展开式中的常数项为（ ）
| 1 | ||
3
|
| A、252 | B、-252 |
| C、84 | D、-84 |
已知角α的终边在函数y=2x（x＞0）的图象上，则1-2sinαcosα-3cos2α的值（ ）
A、-
| ||
B、±
| ||
| C、-2 | ||
| D、±2 |
已知定义域为R的奇函数f（x）的导函数为f′（x），当x≠0时，f′（x）+
＞0，若a=
f（
），b=-2f（-2），c=（ln
）f（ln
），则a，b，c的大小关系正确的是（ ）
| f(x) |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、a＜c＜b |
| B、b＜c＜a |
| C、a＜b＜c |
| D、c＜a＜b |
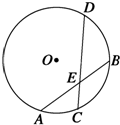如图所示，已知⊙O的半径为5，两弦AB、CD相交于AB的中点E，且AB=8，CE：ED=4：9，则圆心到弦CD的距离为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|