题目内容
已知函数f(x)=2
sinxcosx+2sin2x-1.
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)当x∈[-
,
]时,求函数f(x)的最大值.
| 3 |
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)当x∈[-
| 5π |
| 12 |
| π |
| 6 |
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法,正弦函数的图象
专题:三角函数的求值,三角函数的图像与性质
分析:(Ⅰ)利用两角和公式和二倍角公式对函数解析式化简整理,利用周期公式求得函数最小正周期.
(Ⅱ)利用(Ⅰ)中的函数解析式,根据x的范围利用正弦函数的单调性求得函数的最大值.
(Ⅱ)利用(Ⅰ)中的函数解析式,根据x的范围利用正弦函数的单调性求得函数的最大值.
解答:
解:(Ⅰ)f(x)=2
sinxcosx+2sin2x-1=
sin2x-cos2x=2sin(2x-
)
∴T=
=π,
(Ⅱ)∵x∈[-
,
],
∴2x-
∈[-π,
],
∴sin(2x-
)∈[-1,
],
∴2sin(2x-
)∈[-2,1],
∴函数f(x)的最大值为1.
| 3 |
| 3 |
| π |
| 6 |
∴T=
| 2π |
| 2 |
(Ⅱ)∵x∈[-
| 5π |
| 12 |
| π |
| 6 |
∴2x-
| π |
| 6 |
| π |
| 6 |
∴sin(2x-
| π |
| 6 |
| 1 |
| 2 |
∴2sin(2x-
| π |
| 6 |
∴函数f(x)的最大值为1.
点评:本题主要考查了三角函数恒等变换的应用,三角函数图象与性质.考查了学生基础知识的综合运用.

练习册系列答案
相关题目
设a,b,c均为正数,且x=a+
,y=b+
,z=c+
,则x,y,z三个数( )
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
| A、至少有一个不大于2 |
| B、都小于2 |
| C、至少有一个不小于2 |
| D、都大于2 |
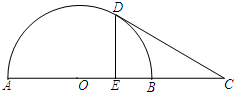 如图,AB是半圆O的直径,延长AB到C,使BC=
如图,AB是半圆O的直径,延长AB到C,使BC= 在圆内接四边形ABCD中,AC与BD交于点E,过点A作圆的切线交CB的延长线于点F.若AB=AD,AF=18,BC=15,求AE的长.
在圆内接四边形ABCD中,AC与BD交于点E,过点A作圆的切线交CB的延长线于点F.若AB=AD,AF=18,BC=15,求AE的长.