题目内容
若(9x-
)n(n∈N*)的展开式的第3项的二项式系数为36,则其展开式中的常数项为( )
| 1 | ||
3
|
| A、252 | B、-252 |
| C、84 | D、-84 |
考点:二项式系数的性质
专题:二项式定理
分析:由条件求得n=9,在二项展开式的通项公式中,令x的幂指数等于0,求出r的值,即可求得常数项.
解答:
解:由题意可得,
=36,∴n=9,
∴(9x-
)n=(9x-
)9(n∈N*)的展开式的通项公式为Tr+1=
•99-r•(-
)r•x9-
,
令9-
=0,求得r=6,故其展开式中的常数项为
•93•(-
)6=84,
故选:C.
| C | 2 n |
∴(9x-
| 1 | ||
3
|
| 1 | ||
3
|
| C | r 9 |
| 1 |
| 3 |
| 3r |
| 2 |
令9-
| 3r |
| 2 |
| C | 6 9 |
| 1 |
| 3 |
故选:C.
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
i是虚数单位,复数
-(1-i)2=( )
| 4+2i |
| 1-2i |
| A、0 | B、2 | C、-4i | D、4i |
在复平面内,复数z和(2-i)i表示的点关于虚轴对称,则复数z=( )
| A、1+2i | B、-1+2i |
| C、-1-2i | D、1-2i |
cos240°=( )
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
若α∈(0,
),β∈(0,π)且tan(a-β)=
,tanβ=-
,则2α-β( )
| π |
| 4 |
| 1 |
| 2 |
| 1 |
| 7 |
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
设a,b,c均为正数,且x=a+
,y=b+
,z=c+
,则x,y,z三个数( )
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
| A、至少有一个不大于2 |
| B、都小于2 |
| C、至少有一个不小于2 |
| D、都大于2 |
已知复数z=
,则|z|=( )
| 5 |
| 1+2i |
| A、1 | ||||
B、
| ||||
C、
| ||||
| D、5 |
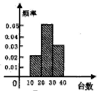
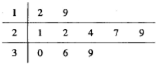 某公司10个销售店某月销售某产品数量(单位:台)的茎叶图如图,分成[11,20),[20,30),[30,39)时,所作的频率分布直方图是( )
某公司10个销售店某月销售某产品数量(单位:台)的茎叶图如图,分成[11,20),[20,30),[30,39)时,所作的频率分布直方图是( )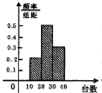


 在圆内接四边形ABCD中,AC与BD交于点E,过点A作圆的切线交CB的延长线于点F.若AB=AD,AF=18,BC=15,求AE的长.
在圆内接四边形ABCD中,AC与BD交于点E,过点A作圆的切线交CB的延长线于点F.若AB=AD,AF=18,BC=15,求AE的长.