题目内容
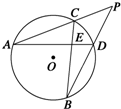如图所示，⊙O的两条弦AD和CB相交于点E，AC和BD的延长线相交于点P，下面结论：①PA•PC=PD•PB；
②PC•CA=PB•BD；
③CE•CD=BE•BA；
④PA•CD=PD•AB．
其中正确的有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
考点：与圆有关的比例线段
专题：选作题,立体几何
分析：利用割线定理、△ABE∽△CDE、△PAD∽△PBC，可得比例线段，即可得出结论．
解答：
解：由割线定理可得PA•PC=PD•PB，即①正确，②不正确；
由△ABE∽△CDE可得AE：CE=AB：CD=BE：DE，∴③不正确；
由△PAD∽△PBC，可得PA：PB=PD：PC═AD：BC，∴④不正确，
故选：A．
由△ABE∽△CDE可得AE：CE=AB：CD=BE：DE，∴③不正确；
由△PAD∽△PBC，可得PA：PB=PD：PC═AD：BC，∴④不正确，
故选：A．
点评：本题考查三角形相似的性质，考查学生分析解决问题的能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
若当P（m，n）为圆x2+（y-1）2=1上任意一点时，不等式m+n+c≥0恒成立，则c的取值范围是（ ）
A、-1-
| ||||
B、
| ||||
C、c≤-
| ||||
D、c≥
|
i是虚数单位，复数
-（1-i）2=（ ）
| 4+2i |
| 1-2i |
| A、0 | B、2 | C、-4i | D、4i |
已知Sn是等差数列{an}（n∈N*）的前n项和，且S6＞S7＞S5，有下列五个结论：
①d＜0；
②S11＞0；
③S12＜0；
④数列{Sn}中的最大项为S11；
⑤数列{Sn}的前n项和Tn中最大为T12．
其中正确的个数是（ ）
①d＜0；
②S11＞0；
③S12＜0；
④数列{Sn}中的最大项为S11；
⑤数列{Sn}的前n项和Tn中最大为T12．
其中正确的个数是（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
在复平面内，复数z和（2-i）i表示的点关于虚轴对称，则复数z=（ ）
| A、1+2i | B、-1+2i |
| C、-1-2i | D、1-2i |
cos240°=（ ）
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
设a，b，c均为正数，且x=a+
，y=b+
，z=c+
，则x，y，z三个数（ ）
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
| A、至少有一个不大于2 |
| B、都小于2 |
| C、至少有一个不小于2 |
| D、都大于2 |
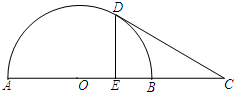如图，AB是半圆O的直径，延长AB到C，使BC=