题目内容
设命题p：存在x∈R，使关于x的不等式x2+2x-m≤0成立；命题q：关于x的方程（4-m）•3x=9x+4有解；若命题p与q有且只有一个为真命题，求实数m的取值范围．
考点：复合命题的真假
专题：简易逻辑
分析：分别化简得出命题p，q；分类讨论：命题p为真，命题q为假；命题p为假，命题q为真，即可得出．
解答：
解：由命题p为真：△=4+4m≥0，得m≥-1．
对于命题q：由（4-m）•3x=9x+4得m=4-(3x+
)≤0，
∴命题q为真时，m≤0．
若命题p为真，命题q为假，则m≥-1且m＞0得m＞0；
若命题p为假，命题q为真，则m＜-1且m≤0得m＜-1；
综上可得：实数m的取值范围为（-∞，-1）∪（0，+∞）．
对于命题q：由（4-m）•3x=9x+4得m=4-(3x+
| 4 |
| 3x |
∴命题q为真时，m≤0．
若命题p为真，命题q为假，则m≥-1且m＞0得m＞0；
若命题p为假，命题q为真，则m＜-1且m≤0得m＜-1；
综上可得：实数m的取值范围为（-∞，-1）∪（0，+∞）．
点评：本题考查了简易逻辑的有关知识、分类讨论思想方法，属于基础题．
练习册系列答案
相关题目
i是虚数单位，复数
-（1-i）2=（ ）
| 4+2i |
| 1-2i |
| A、0 | B、2 | C、-4i | D、4i |
设a，b，c均为正数，且x=a+
，y=b+
，z=c+
，则x，y，z三个数（ ）
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
| A、至少有一个不大于2 |
| B、都小于2 |
| C、至少有一个不小于2 |
| D、都大于2 |
已知复数z=
，则|z|=（ ）
| 5 |
| 1+2i |
| A、1 | ||||
B、
| ||||
C、
| ||||
| D、5 |
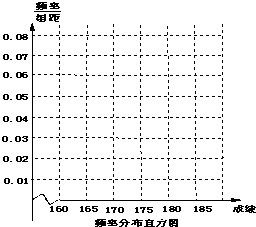某高校在2011年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组，得到的频率分布表如图所示．
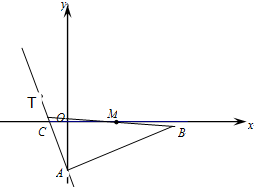如图，在Rt△ABC中，∠A为直角，AB边所在直线的方程为x-3y-6=0，点T（-1，1）在直线AC上，斜边中点为M（2，0）．
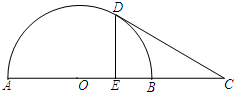如图，AB是半圆O的直径，延长AB到C，使BC=
在圆内接四边形ABCD中，AC与BD交于点E，过点A作圆的切线交CB的延长线于点F．若AB=AD，AF=18，BC=15，求AE的长．