题目内容
设非零向量
,
,
,满足|
+
|=|
-
|,且|
|=|
|=|
+
+
|=1,则|
|的取值范围是( )
| x |
| y |
| z |
| x |
| y |
| x |
| y |
| x |
| y |
| x |
| y |
| z |
| ||||
|
|
| A、[0,2] | ||||||||
B、[1-
| ||||||||
C、[0,
| ||||||||
| D、[1,2] |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:首先,根据|
+
|=|
-
|,得到
•
=0,然后,引入坐标运算,最后结合几何意义进行求解.
| x |
| y |
| x |
| y |
| x |
| y |
解答:
解:∵|
+
|=|
-
|,
∴两边平方,得
2+2
•
+
2=
2-2
•
+
2,
∴
•
=0,
∵|
|=|
|=1,
∴设
=(1,0) ,
=(0,1),
=(m,n)
∴
+
=(1,1),
∵|
+
+
|=1,
∴(m+1)2+(n+1)2=1,
∴向量
的终点组成的轨迹是一个以(-1,-1)为圆心,以1为半径的圆,
设
与
的夹角为θ,
∴则|
|=|
||cosθ|,
cosθ的几何意义为:向量
在向量
方向上的投影,
其绝对值|
||cosθ|∈[0,2],
∴|
|∈[0,2].
故选:A.
| x |
| y |
| x |
| y |
∴两边平方,得
| x |
| x |
| y |
| y |
| x |
| x |
| y |
| y |
∴
| x |
| y |
∵|
| x |
| y |
∴设
| x |
| y |
| z |
∴
| x |
| y |
∵|
| x |
| y |
| z |
∴(m+1)2+(n+1)2=1,
∴向量
| z |
设
| x |
| z |
∴则|
| ||||
|
|
| z |
| z |
| z |
| x |
其绝对值|
| z |
∴|
| ||||
|
|
故选:A.
点评:本题重点考查了向量的坐标表示及其运算、向量的基本运算法则等知识,属于中档题.

练习册系列答案
相关题目
执行如图所示的程序框图(算法流程图),则输出结果是( )


| A、0 | ||
B、
| ||
C、
| ||
D、
|
已知i是虚数单位,复数
=1-bi,其中a、b∈R,则|a+bi|等于( )
| 2-ai |
| i |
| A、-1+2i | ||
| B、1 | ||
C、
| ||
| D、5 |
若当P(m,n)为圆x2+(y-1)2=1上任意一点时,不等式m+n+c≥0恒成立,则c的取值范围是( )
A、-1-
| ||||
B、
| ||||
C、c≤-
| ||||
D、c≥
|
i是虚数单位,复数
-(1-i)2=( )
| 4+2i |
| 1-2i |
| A、0 | B、2 | C、-4i | D、4i |
设a,b,c均为正数,且x=a+
,y=b+
,z=c+
,则x,y,z三个数( )
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
| A、至少有一个不大于2 |
| B、都小于2 |
| C、至少有一个不小于2 |
| D、都大于2 |
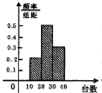
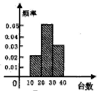
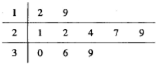 某公司10个销售店某月销售某产品数量(单位:台)的茎叶图如图,分成[11,20),[20,30),[30,39)时,所作的频率分布直方图是( )
某公司10个销售店某月销售某产品数量(单位:台)的茎叶图如图,分成[11,20),[20,30),[30,39)时,所作的频率分布直方图是( )