题目内容
下列函数:①f(x)=-3|x|,②f(x)=x3,③f(x)=
,④f(x)=cos
,⑤f(x)=-2x2+1中,既是偶函数,又是在区间(0,+∞)上单调递减函数为 (写出符合要求的所有函数的序号).
| ln|x| |
| 3 |
| πx |
| 2 |
考点:函数单调性的判断与证明
专题:常规题型,函数的性质及应用
分析:由基本初等函数的性质对5个函数的奇偶性与单调性一一判断.
解答:
解:①是偶函数,且在(0,+∞)上是单调递减函数,故正确;
②是奇函数,不符合题意;
③是偶函数,但在(0,+∞)上是单调递增函数,不符合题意;
④是偶函数,但在(0,+∞)上不单调,不符合题意;
⑤是偶函数,且在(0,+∞)上是单调递减函数,故正确.
故答案为①⑤.
②是奇函数,不符合题意;
③是偶函数,但在(0,+∞)上是单调递增函数,不符合题意;
④是偶函数,但在(0,+∞)上不单调,不符合题意;
⑤是偶函数,且在(0,+∞)上是单调递减函数,故正确.
故答案为①⑤.
点评:本题考查了基本初等函数的变形后的函数的单调性与奇偶性,属于基础题.

练习册系列答案
相关题目
在△ABC中,三个内角分别是A,B,C,若sinC=2cosA•sinB,则此△ABC一定是( )
| A、直角三角形 |
| B、正三角形 |
| C、等腰三角形 |
| D、等腰直角三角形 |
若|
|=|
|=|
•
|,则
与
+
的夹角为( )
| a |
| b |
| a |
| b |
| b |
| a |
| b |
| A、30° | B、60° |
| C、150° | D、120° |
已知椭圆
+y2=1和双曲线
-y2=1共焦点F1,F2,P为两曲线的一个公共点,则∠F1PF2的大小为( )
| x |
| m |
| x2 |
| n2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
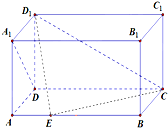 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=