题目内容
已知直角梯形ABCD中，AD∥BC，∠ADC=90°，AD=3，BC=2，P是腰DC上的动点，则|
+3
|的最小值为 ．
| PA |
| PB |
考点：向量在几何中的应用
专题：平面向量及应用
分析：由题意，可利用解析法求解，以直线DA，DC分别为x，y轴建立平面直角坐标系，则A（3，0），B（2，a），C（0，a），D（0，0），设P（0，b）（0≤b≤a），用坐标把
与
表示出来，然后利用模长公式将|
+3
|表示出来，再研究关于a，b的式子如何求最小值的问题，化简后发现结果可利用完全平方式求最小值，问题获解．
| PA |
| PB |
| PA |
| PB |
解答：
解：如图，以直线DA，DC分别为x，y轴建立平面直角坐标系，设CD=a，DP=b，则0≤b≤a．
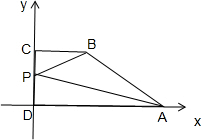
则A（3，0），B（2，a），C（0，a），D（0，0）
设P（0，b）（0≤b≤a），
则
+3
=(3，-b)+3(2，a-b)=(9，3a-4b)，
所以|
+3
|=
≥9，当且仅当3a=4b，即P位于最接近于C的PC的四等分点时，|
+3
|最大．
故答案为：9．
则A（3，0），B（2，a），C（0，a），D（0，0）
设P（0，b）（0≤b≤a），
则
| PA |
| PB |
所以|
| PA |
| PB |
| 81+(3a-4b)2 |
| PA |
| PB |
故答案为：9．
点评：本题考查了利用向量法解决几何问题的思想方法，一般来说先建系，给出所求的、已知的点的坐标，用坐标把已知条件、所求表示出来后，再结合相关知识求解．
练习册系列答案
相关题目