Question

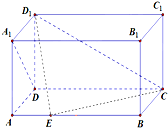如图，在长方体ABCD-A₁B₁C₁D₁中，AD=AA₁=1，AB=

3

，点E在棱AB上．
（1）求异面直线D₁C与A₁D所成的角的余弦值；
（2）当二面角D₁-EC-D的大小为45°时，求点B到面D₁EC的距离．

Answer 1

考点：异面直线及其所成的角

专题：综合题,空间位置关系与距离,空间角

分析：（1）连结B₁C，则∠D₁CB₁是异面直线D₁E与A₁D所成的角，利用余弦定理，求异面直线D₁C与A₁D所成的角的余弦值；
（2）利用VB-CED1=VD1-BCE，得

1

3

•

1

2

CE•D₁F•h=

1

3

•

1

2

BE•BC•DD₁，即可求点B到面D₁EC的距离．

解答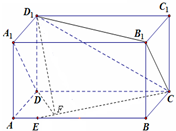： 解：（1）连结B₁C，∵A₁D∥B₁C
∴∠D₁CB₁是异面直线D₁E与A₁D所成的角
在△D₁CB₁中，D₁C=D₁B₁=2，B₁C=

2

，
∴cos∠D₁CB₁=

2

4

∴异面直线D₁C与A₁D所成的角的余弦值为

2

4

．…（5分）
（2）作DF⊥CE，垂足为F，连结D₁F，则CE⊥D₁F．
所以∠DFD₁为二面角D₁-EC-D的平面角，且∠DFD₁=45°．
于是DF=DD₁=1，D₁F=

2

，
所以Rt△BCE≌Rt△FDC，所以CE=CD=

3

，
又BC=1，所以BE=

2

．…（10分）
设点B到平面D₁EC的距离为h，
则由VB-CED1=VD1-BCE，得

1

3

•

1

2

CE•D₁F•h=

1

3

•

1

2

BE•BC•DD₁，
即

3

h=1，∴h=

3

3

．…（12分）

点评：本题主要考查空间异面直线的夹角问题与点到平面的距离，而空间角解决的关键是做角，由图形的结构及题设条件正确作出平面角来，再结合解三角形的有关知识求出答案即可，求点到平面的距离的方法：一般是利用等体积法或者借助于向量求解．