题目内容
17.三棱锥P-ABC的四个顶点都在球O的球面上,已知PA、PB、PC两两垂直,PA=1,PB+PC=4,当三棱锥的体积最大时,球心O到平面ABC的距离是( )| A. | $\frac{\sqrt{6}}{12}$ | B. | $\frac{\sqrt{6}}{6}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{3}{2}$-$\frac{\sqrt{6}}{3}$ |
分析 当且仅当PB=PC=2时,三棱锥的体积最大,如图所示,将P-ABC视为正四棱柱的一部分,求出△ABC外接圆的半径,即可求出球心O到平面ABC的距离.
解答 解:由题意,V=$\frac{1}{3}•\frac{1}{2}•1•PB•PC≤\frac{1}{3}(PB+PC)^{2}$=$\frac{16}{3}$,
当且仅当PB=PC=2时,三棱锥的体积最大,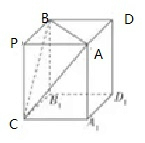
如图所示,将P-ABC视为正四棱柱的一部分,
则CD=2R,即PA2+PB2+PC2=4R2=9,可得R=$\frac{3}{2}$,
因为AB=AC=$\sqrt{5}$,BC=2$\sqrt{2}$,
所以cos∠ACB=$\frac{5+8-5}{2×\sqrt{5}×2\sqrt{2}}$=$\frac{\sqrt{10}}{5}$,sin∠ACB=$\frac{\sqrt{15}}{5}$,
△ABC外接圆的半径为r=$\frac{5\sqrt{3}}{6}$,
设球心到平面ABC的距离为d,
所以d=$\sqrt{\frac{9}{4}-\frac{75}{36}}$=$\frac{\sqrt{6}}{6}$.
故选B.
点评 本题考查球心O到平面ABC的距离,考查三棱锥体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
2.某几何体的三视图如图所示,则该几何体外接球的表面积为( )
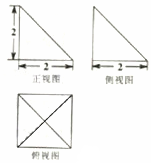

| A. | 4π | B. | 12π | C. | 48π | D. | 6$\sqrt{3}$π |