题目内容
2.某几何体的三视图如图所示,则该几何体外接球的表面积为( )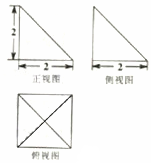
| A. | 4π | B. | 12π | C. | 48π | D. | 6$\sqrt{3}$π |
分析 由三视图可知:该几何体为一个三棱锥P-BCD,作PA⊥底面BCD,垂足为A,底面ABCD是边长为2的正方形.
则该几何体外接球的直径2R=$\sqrt{P{A}^{2}+A{C}^{2}}$.
解答 解:由三视图可知:该几何体为一个三棱锥P-BCD,
作PA⊥底面BCD,垂足为A,底面ABCD是边长为2的正方形.
则该几何体外接球的直径2R=$\sqrt{P{A}^{2}+A{C}^{2}}$=2$\sqrt{3}$.
表面积为=4πR2=12π.
故选:B.
点评 本题考查了四棱锥的三视图、球的表面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
12.执行如图所示的程序框图,则输出的Z值为( )


| A. | 64 | B. | 6 | C. | 8 | D. | 3 |
13.已知关于x的方程2x2-mx+1=0,$x∈[{\frac{1}{2},4}]$存在两个不同的实根,则实数m的取值范围为( )
| A. | (2,3] | B. | $(2\sqrt{2},8\frac{1}{4})$ | C. | $[3,8\frac{1}{4}]$ | D. | $(2\sqrt{2},3]$ |
17.三棱锥P-ABC的四个顶点都在球O的球面上,已知PA、PB、PC两两垂直,PA=1,PB+PC=4,当三棱锥的体积最大时,球心O到平面ABC的距离是( )
| A. | $\frac{\sqrt{6}}{12}$ | B. | $\frac{\sqrt{6}}{6}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{3}{2}$-$\frac{\sqrt{6}}{3}$ |
11.某校校庆期间,大会秘书团计划从包括甲、乙两人在内的七名老师中随机选择4名参加志愿者服务工作,根据工作特点要求甲、乙两人中至少有1人参加,则甲、乙都被选中且列队服务时不相邻的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{4}$ |
12. 某志愿者到某山区小学支教,为了解留守儿童的幸福感,该志愿者对某班40名学生进行了一次幸福指数的调查问卷,并用茎叶图表示如图(注:图中幸福指数低于70,说明孩子幸福感弱;幸福指数不低于70,说明孩子幸福感强).
某志愿者到某山区小学支教,为了解留守儿童的幸福感,该志愿者对某班40名学生进行了一次幸福指数的调查问卷,并用茎叶图表示如图(注:图中幸福指数低于70,说明孩子幸福感弱;幸福指数不低于70,说明孩子幸福感强).
(1)根据茎叶图中的数据完成2×2列联表,并判断能否有95%的把握认为孩子的幸福感强与是否是留守儿童有关?
(2)从15个留守儿童中按幸福感强弱进行分层抽样,共抽取5人,又在这5人中随机抽取2人进行家访,求这2个学生中恰有一人幸福感强的概率.
参考公式:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$.
附表:
 某志愿者到某山区小学支教,为了解留守儿童的幸福感,该志愿者对某班40名学生进行了一次幸福指数的调查问卷,并用茎叶图表示如图(注:图中幸福指数低于70,说明孩子幸福感弱;幸福指数不低于70,说明孩子幸福感强).
某志愿者到某山区小学支教,为了解留守儿童的幸福感,该志愿者对某班40名学生进行了一次幸福指数的调查问卷,并用茎叶图表示如图(注:图中幸福指数低于70,说明孩子幸福感弱;幸福指数不低于70,说明孩子幸福感强).(1)根据茎叶图中的数据完成2×2列联表,并判断能否有95%的把握认为孩子的幸福感强与是否是留守儿童有关?
| 幸福感强 | 幸福感弱 | 总计 | |
| 留守儿童 | 6 | 9 | 15 |
| 非留守儿童 | 18 | 7 | 25 |
| 总计 | 24 | 16 | 40 |
参考公式:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$.
附表:
| P(K2≥k0) | 0.050 | 0.010 |
| k0 | 3.841 | 6.635 |
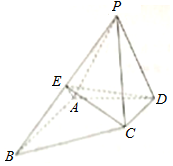 如图,四棱锥P-ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点
如图,四棱锥P-ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点