题目内容
已知函数f(x)=loga
(a>0,a≠1)
(1)求f(x)的定义域;
(2)讨论f(x)的奇偶性.
| x+1 |
| x-1 |
(1)求f(x)的定义域;
(2)讨论f(x)的奇偶性.
考点:对数函数的定义域,对数的运算性质
专题:函数的性质及应用
分析:(1)根据对数的真数要大于0,构造不等式,解不等式可得函数的定义域;
(2)用奇偶性定义,分析f(-x)与f(x)的关系,进而可得f(x)的奇偶性.
(2)用奇偶性定义,分析f(-x)与f(x)的关系,进而可得f(x)的奇偶性.
解答:
解:(1)使f(x)有意义,则
>0,
解得:x>1或x<-1,
∴f(x)的定义域为{x|x>1,或x<-1}.
(2)由(1)知f(x)的定义域关于原点对称,
∵f(-x)=loga
=loga
=loga(
)-1=-loga
=-f(x).
∴f(x)为奇函数.
| x+1 |
| x-1 |
解得:x>1或x<-1,
∴f(x)的定义域为{x|x>1,或x<-1}.
(2)由(1)知f(x)的定义域关于原点对称,
∵f(-x)=loga
| -x+1 |
| -x-1 |
| x-1 |
| x+1 |
| x+1 |
| x-1 |
| x+1 |
| x-1 |
∴f(x)为奇函数.
点评:本题主要考查函数的基本性质--奇偶性和定义域,是函数中的常考题型,属基础题.

练习册系列答案
相关题目
设集合A={y|y=
,x∈R},集合B={y|1≤y<4},则A∩(∁RB)( )
| x-1 |
| A、(0,1)∪[4,+∞) |
| B、[4,+∞) |
| C、(4,+∞) |
| D、∅ |
下列说法中,不正确的是( )
| A、“|x|=|y|”是“x=y”的必要不充分条件 |
| B、命题p:?x∈R,sinx≤1,则¬p:?x∈R,sinx>1 |
| C、“λ≤2”是“数列an=n2-λn+1(n∈N*)为递增数列”的充要条件 |
| D、命题p:所有有理数都是实数,q:正数的对数都是负数,则(¬p)∨(¬q)为真命题 |
设x,y满足约束条件
,则z=2x-y的最大值为( )
|
| A、10 | B、8 | C、3 | D、2 |
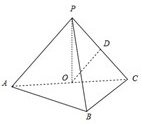 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥平面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥平面ABC.