题目内容
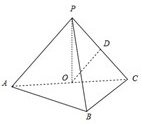 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥平面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥平面ABC.(1)求证:OD∥平面PAB;
(2)当k=
| 1 |
| 2 |
(3)当k为何值时,O在平面PBC内的射影恰好为△PBC的重心.
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:方法一:(Ⅰ)首先利用中位线得出线线平行,进一步利用线面平行的判定定理得出结论.
(Ⅱ)先作出线面角,由题意知,OD∥PA,故可转化为求OD与面PBC的夹角问题,由题设条件知取BC的中点E,连PE,则O在线PE上的垂足必在PE上,设其为F,则可证得∠ODF所求的线面角,下据条件求之.
(Ⅲ)若F是重心,则必有BFD三点共线,又D是中点,故定有BC=PB,可求得k=1.
(Ⅱ)先作出线面角,由题意知,OD∥PA,故可转化为求OD与面PBC的夹角问题,由题设条件知取BC的中点E,连PE,则O在线PE上的垂足必在PE上,设其为F,则可证得∠ODF所求的线面角,下据条件求之.
(Ⅲ)若F是重心,则必有BFD三点共线,又D是中点,故定有BC=PB,可求得k=1.
解答:
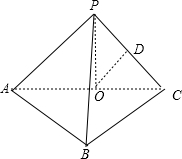 (Ⅰ)证明:在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点
(Ⅰ)证明:在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点
∴OD∥AP
∵AP?平面PAB,OD?平面PAB
∴OD∥平面PAB.
(Ⅱ)∵AB⊥BC OA=OC
∴OA=OB=OC
又∵OP⊥平面ABC
∴PA=PB=PC
取BC的中点E,连结PE,
则:BC⊥平面POE
作OF⊥PE于F,连结DF,
则:DF⊥平面PBC
∴∠ODF是DO与平面PBC所成的角.
由OD∥PA
∴∠ODF是PA与平面PBC所成的角
在Rt△ODG中,sin∠ODF=
=
PA与平面PBC所成的角为:crsin
(Ⅲ)由(Ⅱ)知:OF⊥平面PBC
∴F是O在平面PBC内的射影.
∵D是PC的中点,
若点F是△PBC的重心,
则:B、F、D三点共线.
所以,直线OB在平面PBC内的射影为直线BD.
∵OB⊥PC
PC⊥BD
∴PB=BC
即:k=1
反之,当k=1时,三棱锥O-PBC为正三棱锥.
O在平面PBC内的射影恰好为△PBC的重心
 (Ⅰ)证明:在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点
(Ⅰ)证明:在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点∴OD∥AP
∵AP?平面PAB,OD?平面PAB
∴OD∥平面PAB.
(Ⅱ)∵AB⊥BC OA=OC
∴OA=OB=OC
又∵OP⊥平面ABC
∴PA=PB=PC
取BC的中点E,连结PE,
则:BC⊥平面POE
作OF⊥PE于F,连结DF,
则:DF⊥平面PBC
∴∠ODF是DO与平面PBC所成的角.
由OD∥PA
∴∠ODF是PA与平面PBC所成的角
在Rt△ODG中,sin∠ODF=
| OF |
| OD |
| ||
| 30 |
PA与平面PBC所成的角为:crsin
| ||
| 30 |
(Ⅲ)由(Ⅱ)知:OF⊥平面PBC
∴F是O在平面PBC内的射影.
∵D是PC的中点,
若点F是△PBC的重心,
则:B、F、D三点共线.
所以,直线OB在平面PBC内的射影为直线BD.
∵OB⊥PC
PC⊥BD
∴PB=BC
即:k=1
反之,当k=1时,三棱锥O-PBC为正三棱锥.
O在平面PBC内的射影恰好为△PBC的重心
点评:本题考查的知识要点:线面的夹角问题,及由位置关系转化为方程求参数,重点考查空间想象能力和转化能力.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
sin(
π+x)=( )
| 3 |
| 2 |
| A、sinx | B、cosx |
| C、-sinx | D、-cosx |
若圆锥的轴截面是正三角形,则它的侧面积是底面积的( )
| A、4倍 | ||
| B、3倍 | ||
C、
| ||
| D、2倍 |
若函数f(x)=sin2x-
(x∈R),则f(x)是( )
| 1 |
| 2 |
A、最小正周期为
| ||
| B、最小正周期为π的奇函数 | ||
| C、最小正周期为2π的偶函数 | ||
| D、最小正周期为π的偶函数 |