题目内容
已知函数f(x)=
x2+lnx.
(Ⅰ)求函数f(x)在[1,e]上的最大值、最小值;
(Ⅱ)当x∈[1,+∞),比较f(x)与g(x)=
x3的大小.
(Ⅲ)求证:[f′(x)]n-f′(xn)≥2n-2(n∈N*)
| 1 |
| 2 |
(Ⅰ)求函数f(x)在[1,e]上的最大值、最小值;
(Ⅱ)当x∈[1,+∞),比较f(x)与g(x)=
| 2 |
| 3 |
(Ⅲ)求证:[f′(x)]n-f′(xn)≥2n-2(n∈N*)
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)求f′(x),根据f′(x)的符号判断函数f(x)的单调性,根据单调性求它在[1,e]上的最大、最小值;
(Ⅱ)作差比较f(x),g(x)的大小,所以构造函数F(x)=f(x)-g(x),求F′(x),判断该导数的符号便可判断出F(x)在[1,+∞)上单调递减,所以F(x)≤F(1)=-
<0,所以便得到f(x)<g(x);
(Ⅲ)f′(x)=x+
,所以便得到f′(xn)=xn+
,所以设S=[f′(x)]n-f′(xn)=(x+
)n-xn-
=∁n1xn-1•
+∁n2xn-2•
+…+∁nn-1x•
①;
对该式倒序相加便得到S=∁nn-1x-(n-2)+∁nn-2x-(n-4)+…+∁n1xn-2 ②.①+②得:2S=∁n1[xn-2+x-(n-2)]+∁n2[xn-4+x-(n-4)]+…+∁nn-1[x-(n-2)+xn-2],所以根据基本不等式便可得到:2S≥2(∁n1+∁n2+…+∁nn-1)=2(2n-2),所以S≥2n-2.
(Ⅱ)作差比较f(x),g(x)的大小,所以构造函数F(x)=f(x)-g(x),求F′(x),判断该导数的符号便可判断出F(x)在[1,+∞)上单调递减,所以F(x)≤F(1)=-
| 1 |
| 6 |
(Ⅲ)f′(x)=x+
| 1 |
| x |
| 1 |
| xn |
| 1 |
| x |
| 1 |
| xn |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| xn-1 |
对该式倒序相加便得到S=∁nn-1x-(n-2)+∁nn-2x-(n-4)+…+∁n1xn-2 ②.①+②得:2S=∁n1[xn-2+x-(n-2)]+∁n2[xn-4+x-(n-4)]+…+∁nn-1[x-(n-2)+xn-2],所以根据基本不等式便可得到:2S≥2(∁n1+∁n2+…+∁nn-1)=2(2n-2),所以S≥2n-2.
解答:
解:(I)f′(x)=x+
>0(x>0),∴f(x)在(0,+∞)上是增函数;
∴f(x)在[1,e]的最大值,最小值分别为f(e)=
e2+1,f(1)=
;
(II)设F(x)=f(x)-g(x)=
x2+lnx-
x3,F′(x)=x+
-2x2=
=
∴当x≥1时,F′(x)≤0,即F(x)在[1,+∞)上单调递减;
∴F(x)≤F(1)=-
<0;
∴f(x)<g(x);
(III)f′(x)=x+
,∴[f′(x)]n=(x+
)n,f′(xn)=xn+
;
∴设S=[f′(x)]n-f′(xn)=∁n1xn-1•
+∁n2xn-2•
+…+∁nn-1x•
①;
将上式倒序相加S=∁nn-1x-(n-2)+∁nn-2x-(n-4)+…+∁n1xn-2 ②;
∴①+②得:2S=∁n1[xn-2+x-(n-2)]+∁n2[xn-4+x-(n-4)]+…+∁nn-1[x-(n-2)+xn-2]≥2(∁n1+∁n2+…+∁nn-1);
∴S≥∁n1+∁n2+…+∁nn-1=2n-2;
即[f′(x)]n-f′(xn)≥2n-2.
| 1 |
| x |
∴f(x)在[1,e]的最大值,最小值分别为f(e)=
| 1 |
| 2 |
| 1 |
| 2 |
(II)设F(x)=f(x)-g(x)=
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| x |
| x2+1-2x3 |
| x |
| (1-x)(2x2+x+1) |
| x |
∴当x≥1时,F′(x)≤0,即F(x)在[1,+∞)上单调递减;
∴F(x)≤F(1)=-
| 1 |
| 6 |
∴f(x)<g(x);
(III)f′(x)=x+
| 1 |
| x |
| 1 |
| x |
| 1 |
| xn |
∴设S=[f′(x)]n-f′(xn)=∁n1xn-1•
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| xn-1 |
将上式倒序相加S=∁nn-1x-(n-2)+∁nn-2x-(n-4)+…+∁n1xn-2 ②;
∴①+②得:2S=∁n1[xn-2+x-(n-2)]+∁n2[xn-4+x-(n-4)]+…+∁nn-1[x-(n-2)+xn-2]≥2(∁n1+∁n2+…+∁nn-1);
∴S≥∁n1+∁n2+…+∁nn-1=2n-2;
即[f′(x)]n-f′(xn)≥2n-2.
点评:考查根据函数导数符号判断函数单调性的方法,以及根据单调性求函数的最大值、最小值,构造函数解决问题的方法,以及二项式定理,对于求和的时候所用的倒序相加的方法,及(1+1)n的二项展开式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
sin(
π+x)=( )
| 3 |
| 2 |
| A、sinx | B、cosx |
| C、-sinx | D、-cosx |
i为虚数单位,则(1+i)(1-i)=( )
| A、2 i |
| B、-2 i |
| C、2 |
| D、-2 |
设偶函数f(x)=
sin(2x+φ)-cos(2x+φ)(|φ|<
),则( )
| 3 |
| π |
| 2 |
A、y=f(x)的对称中心为(
| ||||||
B、y=f(x)的对称中心为(
| ||||||
C、y=f(x)的对称中心为(
| ||||||
D、y=f(x)的对称中心为(
|

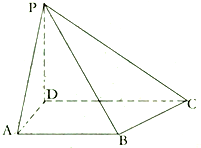 如图,四棱锥P-ABCD中,PD⊥平面ABCD,AB∥CD,∠ADC=90°,且CD=2,AD=
如图,四棱锥P-ABCD中,PD⊥平面ABCD,AB∥CD,∠ADC=90°,且CD=2,AD=