题目内容
已知曲线C1的参数方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2.
(1)求曲线C1、C2的普通方程;
(2)若曲线C1、C2有公共点,求a的取值范围.
|
(1)求曲线C1、C2的普通方程;
(2)若曲线C1、C2有公共点,求a的取值范围.
考点:直线的参数方程,简单曲线的极坐标方程
专题:坐标系和参数方程
分析:(1)由参数方程和普通方程的关系易得曲线C1、C2的普通方程分别为:
x+y-
a=0,x2+y2=4;
(2)由直线和圆的位置关系可得圆心(0,0)到直线
x+y-
a=0的距离d≤2,由距离公式可得d的不等式,解不等式可得.
| 3 |
| 3 |
(2)由直线和圆的位置关系可得圆心(0,0)到直线
| 3 |
| 3 |
解答:
解:(1)∵曲线C1的参数方程为
(t为参数),
∴消去参数t可得
x+y-
a=0,
又曲线C2的极坐标方程为ρ=2,
∴
=2,平方可得x2+y2=4,
∴曲线C1、C2的普通方程分别为:
x+y-
a=0,x2+y2=4;
(2)若曲线C1、C2有公共点,
则圆心(0,0)到直线
x+y-
a=0的距离d≤2,
∴
≤2,解得-
≤a≤
∴a的取值范围为:[-
,
]
|
∴消去参数t可得
| 3 |
| 3 |
又曲线C2的极坐标方程为ρ=2,
∴
| x2+y2 |
∴曲线C1、C2的普通方程分别为:
| 3 |
| 3 |
(2)若曲线C1、C2有公共点,
则圆心(0,0)到直线
| 3 |
| 3 |
∴
|-
| ||
|
4
| ||
| 3 |
4
| ||
| 3 |
∴a的取值范围为:[-
4
| ||
| 3 |
4
| ||
| 3 |
点评:本题考查直线和圆的参数方程,涉及直线和圆的位置关系,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
与y=x为同一个函数的是( )
A、y=
| |||
B、y=
| |||
C、
| |||
D、y=(
|
若圆锥的轴截面是正三角形,则它的侧面积是底面积的( )
| A、4倍 | ||
| B、3倍 | ||
C、
| ||
| D、2倍 |
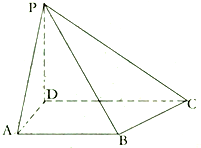 如图,四棱锥P-ABCD中,PD⊥平面ABCD,AB∥CD,∠ADC=90°,且CD=2,AD=
如图,四棱锥P-ABCD中,PD⊥平面ABCD,AB∥CD,∠ADC=90°,且CD=2,AD=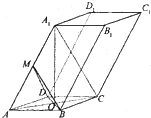 已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形,AC∩BD=O,AA1=2
已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形,AC∩BD=O,AA1=2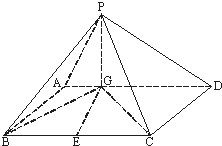 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=
如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=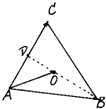 (1)设x,y∈R,向量
(1)设x,y∈R,向量