题目内容
已知函数f(x)=x2-1,g(x)=a|x-1|,F(x)=f(x)-g(x)
(1)若a=2,x∈[0,3],求F(x)值域;
(2)若a>2,解关于x的不等式F(x)≥0.
(1)若a=2,x∈[0,3],求F(x)值域;
(2)若a>2,解关于x的不等式F(x)≥0.
考点:函数的值域
专题:函数的性质及应用
分析:(1)将a=2代入F(x),然后分类讨论去绝对值号,分段求值.
(2)先得到不等式,然后分x≥1和x<1两类讨论解不等式.
(2)先得到不等式,然后分x≥1和x<1两类讨论解不等式.
解答:
解:∵f(x)=x2-1,g(x)=a|x-1|,
∴F(x)=f(x)-g(x)=x2-1-a|x-1|,
(1)若a=2,F(x)=x2-1-2|x-1|,x∈[0,3],
则当x∈[0,1),即x-1<0时,F(x)=x2-1-2(1-x)=x2+2x-3为二次函数,在[0,1]上单调递增,F(x)∈[-3,0),
当x∈[1,3]即x-1≥0时,F(x)=x2-1-2(x-1)=x2-2x+1为二次函数,在[1,3]上单调递增,F(x)∈[0,4],
综上,x∈[0,3],F(x)值域为[-3,0)∪[0,4]=[-3,4]
(2)F(x)=x2-1-a|x-1|,
当a>2时,F(x)≥0得不等立式x2-1-a|x-1|≥0,
当x=1时,F(x)=0,不等式成立,
当x>1时,F(x)≥0即为x2-1-a(x-1)≥0
化简得(x-1)(x+1-a)≥0,
则x≥a-1
又∵a>2,
∴a-1>1,
∴x≥a-1;
当x<1时,F(x)≥0即为x2-1+a(x-1)≥0,
化简得(x-1)(x+1+a)≥0,
则x≤-a-1
又∵a>2,
∴-a-1<-3
∴x≤-a-1,
综上,若a>2,关于x的不等式F(x)≥0的解集为{x|x≥a-1,x=1或x≤-a-1}.
∴F(x)=f(x)-g(x)=x2-1-a|x-1|,
(1)若a=2,F(x)=x2-1-2|x-1|,x∈[0,3],
则当x∈[0,1),即x-1<0时,F(x)=x2-1-2(1-x)=x2+2x-3为二次函数,在[0,1]上单调递增,F(x)∈[-3,0),
当x∈[1,3]即x-1≥0时,F(x)=x2-1-2(x-1)=x2-2x+1为二次函数,在[1,3]上单调递增,F(x)∈[0,4],
综上,x∈[0,3],F(x)值域为[-3,0)∪[0,4]=[-3,4]
(2)F(x)=x2-1-a|x-1|,
当a>2时,F(x)≥0得不等立式x2-1-a|x-1|≥0,
当x=1时,F(x)=0,不等式成立,
当x>1时,F(x)≥0即为x2-1-a(x-1)≥0
化简得(x-1)(x+1-a)≥0,
则x≥a-1
又∵a>2,
∴a-1>1,
∴x≥a-1;
当x<1时,F(x)≥0即为x2-1+a(x-1)≥0,
化简得(x-1)(x+1+a)≥0,
则x≤-a-1
又∵a>2,
∴-a-1<-3
∴x≤-a-1,
综上,若a>2,关于x的不等式F(x)≥0的解集为{x|x≥a-1,x=1或x≤-a-1}.
点评:解题的关键在两点,一是去绝对值号,二是对参数a的理解.

练习册系列答案
相关题目
i为虚数单位,则(1+i)(1-i)=( )
| A、2 i |
| B、-2 i |
| C、2 |
| D、-2 |
若圆锥的轴截面是正三角形,则它的侧面积是底面积的( )
| A、4倍 | ||
| B、3倍 | ||
C、
| ||
| D、2倍 |
(理做)已知函数f(x)=
-lnx,函数y=f(|x|)的零点个数为n,则n=( )
| 1 |
| x-1 |
| A、2 | B、4 | C、6 | D、8 |

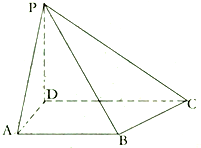 如图,四棱锥P-ABCD中,PD⊥平面ABCD,AB∥CD,∠ADC=90°,且CD=2,AD=
如图,四棱锥P-ABCD中,PD⊥平面ABCD,AB∥CD,∠ADC=90°,且CD=2,AD=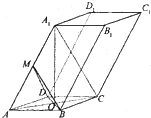 已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形,AC∩BD=O,AA1=2
已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形,AC∩BD=O,AA1=2