题目内容

直线y=2x+m与椭圆
x2
4
+y2=1相交于A、B两点，m为变量，求|AB|的最大值．
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：把y=2x+m与椭圆
x2
4
+y2=1，得：17x2+16mx+4m2-4=0，利用椭圆弦长公式能求出|AB|的最大值．
解答： 解：把y=2x+m与椭圆
x2
4
+y2=1，得：
17x2+16mx+4m2-4=0，
设A（x1，2x1+m），B（x2，2x2+m），
∵直线y=2x+m与椭圆
x2
4
+y2=1相交于A、B两点，
∴x1+x2=-
16m
17
，x1x2=
4m2-4
17
，
△=256m2-68（4m2-4）＞0，
解得-
17
＜m＜
17
，
∴|AB|=
(1+4)[(-
16m
17
)2-4×
4m2-4
17
]

=
1008m2+272
17

≤
1008×(
17
)2+272
17
=
4
1054
17
．
∴|AB|的最大值为
4
1054
17
．
点评：本题考查弦长的最大值的求法，是中档题，解题时要注意椭圆弦长公式的合理运用．
练习册系列答案
相关题目
下列函数是奇函数的是（　　）
A、f（x）=-|x|
B、f（x）=lg（1+x）-lg（1-x）
C、f（x）=2x+2-x
D、f（x）=x3-1
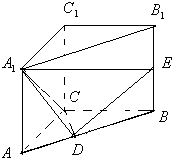已知直三棱柱ABC-A1B1C1中，∠ACB=
π
2
．AC=CB=AA1=2，E为BB1的中点，D在AB上，且∠A1DE=
π
2
．
（Ⅰ）求证：CD⊥面ABB1A1；
（Ⅱ）求二面角D-A1C-A的正弦值．
已知双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）过点P(
2
，
3
)，且离心率为2，过右焦点F作两渐近线的垂线，垂足分别为M，N．
（1）求双曲线C的方程；
（2）求四边形OMFN的面积（O为坐标原点）．
如图所示，已知椭圆C1和抛物线C2有公共焦点F（1，0），C1的中心和C2的顶点都在坐标原点，过点M（4，0）的直线l与抛物线C2分别相交于A、B两点．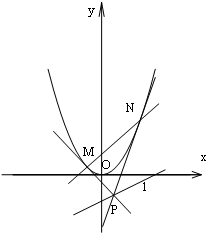
（Ⅰ）写出抛物线C2的标准方程；
（Ⅱ）求证：以AB为直径的圆过原点；
（Ⅲ）若坐标原点O关于直线l的对称点P在抛物线C2上，直线l与椭圆C1有公共点，求椭圆C1的长轴长的最小值．
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左右焦点为F1、F2，点P为椭圆上动点，弦PA、PB分别过点F1、F2，设向量
PF1
=λ1
F1A
，
PF2
=λ2
F2B
，求证：λ1+λ2为定值．
已知f（x）=lnx，g（x）=af（x）+f′（x），
（1）求g（x）的单调区间；
（2）当a=1时，
    ①比较g(x)与g(
1
x
)的大小；
    ②是否存在x0＞0，使得|g（x）-g（x0）|＜
1
x
对任意x＞0成立？若存在，求出x0的取值范围；若不存在，请说明理由．
已知抛物线C：y=x2，直线l：x-2y-2=0，点P是直线l上任意一点，过点P作抛物线C的切线PM，PN，切点分别为M，N，直线PM，PN斜率分别为k1，k2，如图所示
（1）若P（4，1），求证：k1+k2=16；
（2）若MN过抛物线的焦点，求点P的坐标．
抛物线y2=8x的焦点为F，其准线与x轴的交点为M，抛物线上的点P满足
|PF|
|PM|
=
2
2
，O为坐标原点，则|PO|=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网