题目内容
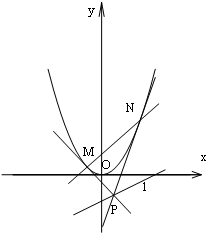 已知抛物线C:y=x2,直线l:x-2y-2=0,点P是直线l上任意一点,过点P作抛物线C的切线PM,PN,切点分别为M,N,直线PM,PN斜率分别为k1,k2,如图所示
已知抛物线C:y=x2,直线l:x-2y-2=0,点P是直线l上任意一点,过点P作抛物线C的切线PM,PN,切点分别为M,N,直线PM,PN斜率分别为k1,k2,如图所示(1)若P(4,1),求证:k1+k2=16;
(2)若MN过抛物线的焦点,求点P的坐标.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设过P的切线方程:y-1=k(x-4),代入抛物线C得:x2-kx+4k-1=0,由△=0,能证明k1+k2=16.
(2)设MN:y=kx+
,代入抛物线方程得x2-kx-
=0,设M(x1,y1),N(x2,y2),对y=x2求导数,求出直线PM和直线PN的方程,由此能求出点P的坐标.
(2)设MN:y=kx+
| 1 |
| 4 |
| 1 |
| 4 |
解答:
(本小题12分)
(1)证明:设过P的切线方程为:y-1=k(x-4),
代入抛物线C,消去y得:x2-kx+4k-1=0,
由△=k2-4(4k-1)=0,∴k2-16k+4=0,
∵该方程的两个根为直线PM,PN斜率k1,k2,
∴k1+k2=16.(5分)
(2)解:∵抛物线的焦点(0,
),∴设MN:y=kx+
,
代入抛物线方程消去y得:x2-kx-
=0,
设M(x1,y1),N(x2,y2),
∴x1+x2=k,x1x2=-
,
对y=x2求导数,y'=2x,∴k1=2x1,k2=2x2,
∴直线PM:y-y1=2x1(x-x1),直线PN:y-y2=2x2(x-x2),
∴点P(k,-
),∵P在直线l上,∴k=
,
∴P(
,-
).(12分)
(1)证明:设过P的切线方程为:y-1=k(x-4),
代入抛物线C,消去y得:x2-kx+4k-1=0,
由△=k2-4(4k-1)=0,∴k2-16k+4=0,
∵该方程的两个根为直线PM,PN斜率k1,k2,
∴k1+k2=16.(5分)
(2)解:∵抛物线的焦点(0,
| 1 |
| 4 |
| 1 |
| 4 |
代入抛物线方程消去y得:x2-kx-
| 1 |
| 4 |
设M(x1,y1),N(x2,y2),
∴x1+x2=k,x1x2=-
| 1 |
| 4 |
对y=x2求导数,y'=2x,∴k1=2x1,k2=2x2,
∴直线PM:y-y1=2x1(x-x1),直线PN:y-y2=2x2(x-x2),
∴点P(k,-
| 1 |
| 4 |
| 3 |
| 2 |
∴P(
| 3 |
| 2 |
| 1 |
| 4 |
点评:本题考查两直线斜率和为16的证明,考查点的坐标的求法,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知三点A(2,1),B(1,-2),C(
,-
),动点P(a,b)满足0≤
•
≤2,且0≤
•
≤2,则点P到点C的距离大于
的概率为( )
| 3 |
| 5 |
| 1 |
| 5 |
| OP |
| OA |
| OP |
| OB |
| 1 |
| 5 |
A、
| ||
B、1-
| ||
C、
| ||
D、1-
|