题目内容
16.设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线与直线x=-1的一个交点的纵坐标为y0,若|y0|<2,则双曲线C的离心率的取值范围是( )| A. | (1,$\sqrt{3}$) | B. | (1,$\sqrt{5}$) | C. | ($\sqrt{3}$,+∞) | D. | ($\sqrt{5}$,+∞) |
分析 求出直线和渐近线的交点的纵坐标,根据不等式关系求出a,b的范围,进行求解即可.
解答 解:∵双曲线的渐近线为y=±$\frac{b}{a}$x,
∴当x=-1时,y=±$\frac{b}{a}$,
∵交点的纵坐标为y0,若|y0|<2,
∴|$\frac{b}{a}$|<2,
则离心率e=$\frac{c}{a}$=$\sqrt{\frac{{c}^{2}}{{a}^{2}}}$=$\sqrt{\frac{{a}^{2}+{b}^{2}}{{a}^{2}}}$=$\sqrt{1+(\frac{b}{a})^{2}}$$<\sqrt{1+4}$=$\sqrt{5}$,
∵e>1,
∴1<e<$\sqrt{5}$,
故选:B
点评 本题主要考查双曲线离心率的计算,根据交点坐标的取值范围建立不等式关系是解决本题的关键.

练习册系列答案
相关题目
8.如图,给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{99}$+$\frac{1}{101}$的值的一个程序框图,判断框内应填入的条件是( )

| A. | i<101? | B. | i>101? | C. | i≤101? | D. | i≥101? |
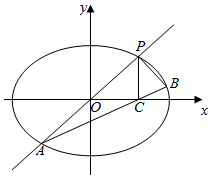 已知椭圆w:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,$\sqrt{2}$),椭圆w上任意一点到两焦点的距离之和为4.
已知椭圆w:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,$\sqrt{2}$),椭圆w上任意一点到两焦点的距离之和为4.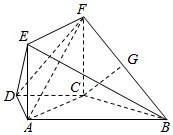 如图,在梯形ABCD中,AB∥CD,AB=2AD=2DC=2CB=2,四边形ACFE是矩形,AE=1,平面ACFE⊥平面ABCD,点G是BF的中点.
如图,在梯形ABCD中,AB∥CD,AB=2AD=2DC=2CB=2,四边形ACFE是矩形,AE=1,平面ACFE⊥平面ABCD,点G是BF的中点.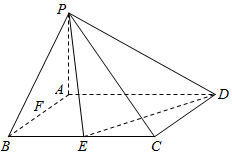 在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=2AB,E,F是线段BC,AB的中点.
在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=2AB,E,F是线段BC,AB的中点.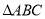 中,
中,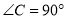 ,点
,点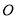 在
在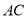 上,以
上,以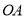 为半径的
为半径的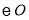 交
交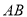 于点
于点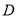 ,
,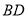 的垂直平分线交
的垂直平分线交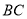 于点
于点 ,交
,交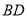 于点
于点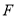 ,连接
,连接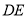 .
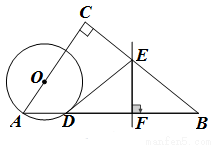
.
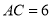 ,
,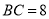 ,
, ,求线段
,求线段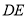 的长.
的长.