题目内容
5.已知等比数列{an}满足an+1+an=10•4n-1(n∈N*),数列{bn}的前n项和为Sn,且bn=log2an.(I)求bn,Sn;
(Ⅱ)设${c_n}={b_n}•({\frac{{2{S_n}}}{n}+1})$,求数列$\left\{{{a_n}+\frac{1}{c_n}}\right\}$的前n项和Tn.
分析 (I)通过在an+1+an=10•4n-1(n∈N*)中分别令n=1、2计算可知等比数列{an}前三项的值,进而可知an=22n-1,根据对数的性质可知bn=2n-1,利用公式计算即得结论;
(Ⅱ)通过(I)裂项、并项相加可知数列{$\frac{1}{{c}_{n}}$}的前n项和,利用等比数列的求和公式可知数列{an}的前n项和,两者相加即得结论.
解答 解:(I)在an+1+an=10•4n-1(n∈N*)中分别令n=1、2可知:
a1+a2=10,a2+a3=40,
又∵a1,a2,a3构成等比数列,
∴a1=2,a2=8,a3=32,
∴an=2•4n-1=22n-1,bn=log2an=bn=log222n-1=2n-1,
Sn=$\frac{n(1+2n-1)}{2}$=n2;
(Ⅱ)由(I)可知${c_n}={b_n}•({\frac{{2{S_n}}}{n}+1})$=(2n-1)•(2n+1),
∴$\frac{1}{{c}_{n}}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),
由等比数列的求和公式可知,数列{an}的前n项和为$\frac{2(1-{4}^{n})}{1-4}$=$\frac{2({4}^{n}-1)}{3}$,
并项相加可知,数列{$\frac{1}{{c}_{n}}$}的前n项和为$\frac{1}{2}$(1-$\frac{1}{2n+1}$)=$\frac{n}{2n+1}$,
从而Tn=$\frac{2({4}^{n}-1)}{3}$+$\frac{n}{2n+1}$.
点评 本题考查数列的通项及前n项和,考查裂项相消法,考查分组求和法,注意解题方法的积累,属于中档题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
16.已知sin(x+$\frac{π}{2}$)=$\frac{1}{3}$,则cos2x=( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{7}{9}$ | D. | $\frac{7}{9}$ |
16.将双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1的右焦点、右顶点、虚轴的一个端点所组成的三角形叫做双曲线的“黄金三角形”,则双曲线C:x2-y2=4的“黄金三角形”的面积是( )
| A. | $\sqrt{2}$-1 | B. | 2$\sqrt{2}$-2 | C. | 1 | D. | 2 |
13.各项均为正数的等差数列{an}中,2a6+2a8=a72,则a7=( )
| A. | 2 | B. | 4 | C. | 16 | D. | 0 |
16.设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线与直线x=-1的一个交点的纵坐标为y0,若|y0|<2,则双曲线C的离心率的取值范围是( )
| A. | (1,$\sqrt{3}$) | B. | (1,$\sqrt{5}$) | C. | ($\sqrt{3}$,+∞) | D. | ($\sqrt{5}$,+∞) |
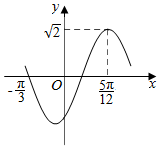 曲线f(x)=$\sqrt{2}$sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,曲线f(x)的解析式为f(x)=$\sqrt{2}$sin(2x-$\frac{π}{3}$).
曲线f(x)=$\sqrt{2}$sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,曲线f(x)的解析式为f(x)=$\sqrt{2}$sin(2x-$\frac{π}{3}$). 如图,在四棱锥P-ABCD中,平面PBC⊥平面ABCD,PB=PC=$\sqrt{2}$,E是PB的中点,AD∥BC,AD⊥CD,BC=2CD=2AD=2.
如图,在四棱锥P-ABCD中,平面PBC⊥平面ABCD,PB=PC=$\sqrt{2}$,E是PB的中点,AD∥BC,AD⊥CD,BC=2CD=2AD=2.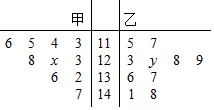 在某校统考中,甲、乙两班数学学科前10名的成绩如表:
在某校统考中,甲、乙两班数学学科前10名的成绩如表: