题目内容
8.如图,给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{99}$+$\frac{1}{101}$的值的一个程序框图,判断框内应填入的条件是( )
| A. | i<101? | B. | i>101? | C. | i≤101? | D. | i≥101? |
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输出S的值.
解答 解:程序运行过程中,各变量值如下表所示:
第1次循环:S=0+1,i=1,
第2次循环:S=1+$\frac{1}{3}$,i=3,
第3次循环:S=1+$\frac{1}{3}$+$\frac{1}{5}$,i=5,…
依此类推,第51次循环:S=1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{101}$,i=101,退出循环
其中判断框内应填入的条件是:i≤101,
故选:C.
点评 本题考查了当型循环结构的应用问题,解题时应准确理解流程图的含义,是基础题目.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
16.将双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1的右焦点、右顶点、虚轴的一个端点所组成的三角形叫做双曲线的“黄金三角形”,则双曲线C:x2-y2=4的“黄金三角形”的面积是( )
| A. | $\sqrt{2}$-1 | B. | 2$\sqrt{2}$-2 | C. | 1 | D. | 2 |
3.已知0<θ<$\frac{π}{2}$,f(θ)=1+m+m($\frac{cosθ-1}{sinθ}$)+$\frac{sinθ-1}{cosθ}$(m>0),则使得f(θ)有最大值时的m的取值范围是( )
| A. | ($\frac{1}{2}$,2) | B. | ($\frac{1}{3}$,3) | C. | [1,3] | D. | [$\frac{1}{4}$,1] |
13.各项均为正数的等差数列{an}中,2a6+2a8=a72,则a7=( )
| A. | 2 | B. | 4 | C. | 16 | D. | 0 |
16.设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线与直线x=-1的一个交点的纵坐标为y0,若|y0|<2,则双曲线C的离心率的取值范围是( )
| A. | (1,$\sqrt{3}$) | B. | (1,$\sqrt{5}$) | C. | ($\sqrt{3}$,+∞) | D. | ($\sqrt{5}$,+∞) |
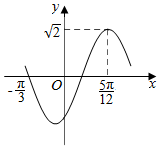 曲线f(x)=$\sqrt{2}$sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,曲线f(x)的解析式为f(x)=$\sqrt{2}$sin(2x-$\frac{π}{3}$).
曲线f(x)=$\sqrt{2}$sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,曲线f(x)的解析式为f(x)=$\sqrt{2}$sin(2x-$\frac{π}{3}$).