题目内容
1.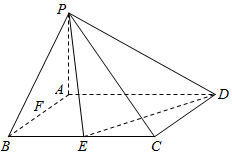 在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=2AB,E,F是线段BC,AB的中点.
在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=2AB,E,F是线段BC,AB的中点.(Ⅰ)证明:ED⊥PE;
(Ⅱ)在线段PA上确定点G,使得FG∥平面PED,请说明理由.
分析 (Ⅰ)由PA⊥平面ABCD先证明DE⊥PA.连接AE,由勾股定理证明DE⊥AE,通过证明DE⊥平面PAE,即可得证PE⊥ED.
(Ⅱ)过点F作FH∥ED交AD于点H,再过点H作HG∥DP交PA于点G,通过证明平面GEH∥平面PFD,然后证明EG∥平面PFD.
解答  (本题满分为12分)
(本题满分为12分)
解:(Ⅰ)证明:由PA⊥平面ABCD,得DE⊥PA.连接AE,
因为AD=2AB,
所以由勾股定理可得DE⊥AE.
所以DE⊥平面PAE,
因此PE⊥ED. …(6分)
(Ⅱ)过点F作FH∥ED交AD于点H,则FH∥平面PED,且有AH=$\frac{1}{4}$AD.
再过点H作HG∥DP交PA于点G,则HG∥平面PED,且AG=$\frac{1}{4}$AP.
由面面平行的判定定理可得平面GEH∥平面PFD,
进而由面面平行的性质得到EG∥平面PFD,
从而确定G点位置. …(12分)
点评 本题主要考查了直线与平面平行的判定,直线与平面垂直的性质,考查了逻辑推理能力和空间想象能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知(1-2x)5=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5,则a3+a4等于( )
| A. | 0 | B. | -240 | C. | -480 | D. | 960 |
13.各项均为正数的等差数列{an}中,2a6+2a8=a72,则a7=( )
| A. | 2 | B. | 4 | C. | 16 | D. | 0 |
16.设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线与直线x=-1的一个交点的纵坐标为y0,若|y0|<2,则双曲线C的离心率的取值范围是( )
| A. | (1,$\sqrt{3}$) | B. | (1,$\sqrt{5}$) | C. | ($\sqrt{3}$,+∞) | D. | ($\sqrt{5}$,+∞) |
6.从抛物线y2=4x的准线l上一点P引抛物线的两条切线PA,PB,A,B为切点,若直线AB的倾斜角为$\frac{π}{3}$,则P点的纵坐标为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | 2$\sqrt{3}$ |
9.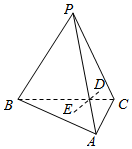 三棱锥P-ABC中,D、E分别是三角形PAC和三角形ABC的外心,则下列判断一定正确的是( )
三棱锥P-ABC中,D、E分别是三角形PAC和三角形ABC的外心,则下列判断一定正确的是( )
 三棱锥P-ABC中,D、E分别是三角形PAC和三角形ABC的外心,则下列判断一定正确的是( )
三棱锥P-ABC中,D、E分别是三角形PAC和三角形ABC的外心,则下列判断一定正确的是( )| A. | DE∥PB | B. | 当AB=BC且PA=AC时DE∥PB | ||
| C. | 当且仅当AB=BC且PA=AC时,DE⊥AC | D. | DE⊥AC |
 如图,在四棱锥P-ABCD中,平面PBC⊥平面ABCD,PB=PC=$\sqrt{2}$,E是PB的中点,AD∥BC,AD⊥CD,BC=2CD=2AD=2.
如图,在四棱锥P-ABCD中,平面PBC⊥平面ABCD,PB=PC=$\sqrt{2}$,E是PB的中点,AD∥BC,AD⊥CD,BC=2CD=2AD=2.