题目内容
8.已知田径队有男运动员56人,女运动员42人,若按男女比例用分层抽样的方法,从全体运动员中抽出14人参加比赛,则抽到女运动员的人数为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 先求出每个个体被抽到的概率,再用女运动员的人数乘以此概率,即得所求.
解答 解:每个个体被抽到的概率等于$\frac{14}{56+42}$=$\frac{1}{7}$,
则样本中女运动员的人数为 42×$\frac{1}{7}$=6.
故选:C.
点评 本题考查了分层抽样的应用问题,用每层的个体数乘以每个个体被抽到的概率得出该层应抽取的个体数.

练习册系列答案
相关题目
16.设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线与直线x=-1的一个交点的纵坐标为y0,若|y0|<2,则双曲线C的离心率的取值范围是( )
| A. | (1,$\sqrt{3}$) | B. | (1,$\sqrt{5}$) | C. | ($\sqrt{3}$,+∞) | D. | ($\sqrt{5}$,+∞) |
20.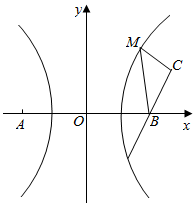 如图,M是以A、B为焦点的双曲线x2-y2=2右支上任一点,若点M到点C(3,1)与点B的距离之和为S,则S的取值范围是( )
如图,M是以A、B为焦点的双曲线x2-y2=2右支上任一点,若点M到点C(3,1)与点B的距离之和为S,则S的取值范围是( )
 如图,M是以A、B为焦点的双曲线x2-y2=2右支上任一点,若点M到点C(3,1)与点B的距离之和为S,则S的取值范围是( )
如图,M是以A、B为焦点的双曲线x2-y2=2右支上任一点,若点M到点C(3,1)与点B的距离之和为S,则S的取值范围是( )| A. | [$\sqrt{26}$+$\sqrt{2}$,+∞) | B. | [$\sqrt{26}$-$2\sqrt{2}$,+∞) | C. | [$\sqrt{26}$-$2\sqrt{2}$,$\sqrt{26}$+$2\sqrt{2}$) | D. | [$\sqrt{26}$-$\sqrt{2}$,+∞) |
16.点E是正方形ABCD的边DC的中点,F是BE中点,且$\overrightarrow{AB}$=$\overrightarrow{a}$.$\overrightarrow{AD}$=$\overrightarrow{b}$.则$\overrightarrow{DF}$=( )
| A. | $\frac{1}{2}\overrightarrow{a}$-$\frac{3}{4}$$\overrightarrow{b}$ | B. | $\frac{1}{2}\overrightarrow{b}$-$\frac{3}{4}\overrightarrow{a}$ | C. | $\frac{3}{4}\overrightarrow{b}$-$\frac{1}{2}\overrightarrow{a}$ | D. | $\frac{3}{4}\overrightarrow{a}$-$\frac{1}{2}\overrightarrow{b}$ |
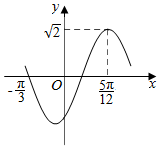 曲线f(x)=$\sqrt{2}$sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,曲线f(x)的解析式为f(x)=$\sqrt{2}$sin(2x-$\frac{π}{3}$).
曲线f(x)=$\sqrt{2}$sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,曲线f(x)的解析式为f(x)=$\sqrt{2}$sin(2x-$\frac{π}{3}$).