题目内容
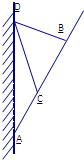 某固定在墙上的广告金属支架如图所示,根据要求,AB至少长3米,C为AB的中点,B到D的距离比CD的长小0.5米,∠BCD=60°
某固定在墙上的广告金属支架如图所示,根据要求,AB至少长3米,C为AB的中点,B到D的距离比CD的长小0.5米,∠BCD=60°(1)若CD=x,BC=y,将支架的总长度表示为y的函数,并写出函数的定义域.(注:支架的总长度为图中线段AB、BD和CD长度之和)
(2)如何设计AB,CD的长,可使支架总长度最短.
考点:解三角形的实际应用
专题:应用题,不等式的解法及应用
分析:(1)△BCD中,CD=x,BC=y,∠BCD=60°,由余弦定理可得x,y的关系式;
(2)设y-1=t(t≥0.5),则原式l=4t+
+5.5,利用基本不等式求出结果.
(2)设y-1=t(t≥0.5),则原式l=4t+
| 1.5 |
| t |
解答:
解:(1)由CD=x,则BD=x-0.5,设BC=y,
则支架的总长度为AC+BC+BD+CD,
在△BCD中,由余弦定理x2+y2-2xycos60°=(x-0.5)2,
化简得 y2-xy+x-0.25=0,即x=
①…(4分)
记l=y+y+x-0.5+x=2y+2x-0.5=
-0.5(-0.5<x<0.5或x>1)---------(6分)
(2)由题中条件得2y≥3,即y≥1.5,设y-1=t(t≥0.5)
则原式l=4t+
+5.5 …(10分)
∵t≥0.5,∴由基本不等式4t+
≥2
有且仅当4t=
,即t=
时成立,
∴y=
+1,∴x=
,
∴当AB=
+2,CD=
时,金属支架总长度最短. …(16分)
则支架的总长度为AC+BC+BD+CD,
在△BCD中,由余弦定理x2+y2-2xycos60°=(x-0.5)2,
化简得 y2-xy+x-0.25=0,即x=
| y2-0.25 |
| y-1 |
记l=y+y+x-0.5+x=2y+2x-0.5=
| 4y2-2y-0.5 |
| y-1 |
(2)由题中条件得2y≥3,即y≥1.5,设y-1=t(t≥0.5)
则原式l=4t+
| 1.5 |
| t |
∵t≥0.5,∴由基本不等式4t+
| 1.5 |
| t |
| 6 |
有且仅当4t=
| 1.5 |
| t |
| ||
| 4 |
∴y=
| ||
| 4 |
3
| ||
| 4 |
∴当AB=
| ||
| 2 |
8+3
| ||
| 4 |
点评:本题借助三角形的余弦定理建立函数解析式,考查函数的最值问题,是中档题.

练习册系列答案
相关题目
(x+1)5展开式的二项式系数的和是( )
| A、6 | B、128 | C、32 | D、64 |
下列函数中,既是偶函数又在区间(-∞,0)上单调递减的是( )
A、f(x)=
| ||
| B、f(x)=x2+1 | ||
| C、f(x)=x3 | ||
| D、f(x)=2-x |
已知M={-3,-2,0,1,2},N={-2,-1,1,2},则M∩N=( )
| A、{-2,1,2 } |
| B、{-3,-2,-1,0,1,2} |
| C、M |
| D、N |
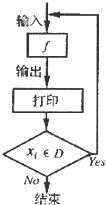 对任意函数f(x),x∈D,可按图示构造一个数列发生器,其工作原理如下:
对任意函数f(x),x∈D,可按图示构造一个数列发生器,其工作原理如下: