题目内容
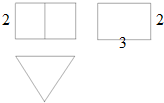
如图，网格纸上小正方形的边长为1，实线画出的是某几何体的三视图，则此几何体的体积为（ ）| A、6 | B、9 | C、12 | D、18 |
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：通过三视图判断几何体的特征，利用三视图的数据求出几何体的体积即可．
解答：
解：该几何体是三棱锥，底面是俯视图，三棱锥的高为4；
底面三角形斜边长为6，高为3的等腰直角三角形，
此几何体的体积为V=
×
×6×3×4=12．
故选C．
底面三角形斜边长为6，高为3的等腰直角三角形，
此几何体的体积为V=
| 1 |
| 3 |
| 1 |
| 2 |
故选C．
点评：本题考查三视图与几何体的关系，考查几何体的体积的求法，考查计算能力．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
（x+1）5展开式的二项式系数的和是（ ）
| A、6 | B、128 | C、32 | D、64 |
一个正三棱柱的三视图如图所示，则这个正三棱柱的侧面积为（ ）
| A、18 | ||
B、6
| ||
C、12
| ||
D、18
|