题目内容
已知f(x)=|ax+1|,a≠0,不等式f(x)≤3的解集是{x|-1≤x≤2}
(1)求a的值;
(2)若g(x)=
,g(x)<|k|存在实数解,求实数k的取值范围.
(1)求a的值;
(2)若g(x)=
| f(x)+f(-x) |
| 2 |
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(1)由|ax+1|≤3得:-4≤ax≤2;分a>0与a<0讨论,结合已知原不等式的解集是{x|-1≤x≤2},即可求得a的值;
(2)易求g(x)=|x-
|+|x+
,依题意,g(x)<|k|存在实数解,只需|k|大于g(x)的最小值,而g(x)=|x-
|+|x+
,≥|x-
-(x+
)|=1,从而去解不等式|k|>1即可.
(2)易求g(x)=|x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)由|ax+1|≤3得:-4≤ax≤2;
当a>0时,-
≤x≤
,∵原不等式的解集是{x|-1≤x≤2},
∴
,该方程组无解;
当a<0时,
≤x≤-
,原不等式的解集是{x|-1≤x≤2},
∴
,解得a=-2.…(5分)
(2)由题:g(x)=
=
=|x-
|+|x+
|,
因为g(x)<|k|存在实数解,只需|k|大于g(x)的最小值,
由绝对值的几何意义,g(x)=|x-
|+|x+
|≥|x-
-(x+
)|=1,所以|k|>1.
解得:k<-1或k>1…(10分)
当a>0时,-
| 4 |
| a |
| 2 |
| a |
∴
|
当a<0时,
| 2 |
| a |
| 4 |
| a |
∴
|
(2)由题:g(x)=
| f(x)+f(-x) |
| 2 |
| |-2x+1|+|2x+1| |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
因为g(x)<|k|存在实数解,只需|k|大于g(x)的最小值,
由绝对值的几何意义,g(x)=|x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:k<-1或k>1…(10分)
点评:本题考查绝对值不等式的解法,着重考查分类讨论思想与等价转化思想的综合应用,考查运算求解能力,属于中档题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
设点P在曲线y=
ex上,点Q在曲线y=ln(2x)上,则|PQ|的最小值为( )
| 1 |
| 2 |
| A、1-ln 2 | ||
B、
| ||
| C、1+ln 2 | ||
D、
|
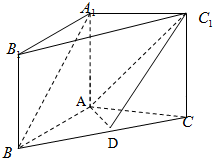 在三棱柱A1B1C1-ABC中,A1A⊥平面ABC,A1A=AB=AC=2,BC=2
在三棱柱A1B1C1-ABC中,A1A⊥平面ABC,A1A=AB=AC=2,BC=2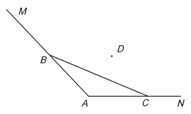 在一个六角形体育馆的一角MAN内,用长为a的围栏设置一个运动器材储存区域(如图所示),已知∠A=120°,B是墙角线AM上的一点,C是墙角线AN上的一点.
在一个六角形体育馆的一角MAN内,用长为a的围栏设置一个运动器材储存区域(如图所示),已知∠A=120°,B是墙角线AM上的一点,C是墙角线AN上的一点.