题目内容
设点P在曲线y=
ex上,点Q在曲线y=ln(2x)上,则|PQ|的最小值为( )
| 1 |
| 2 |
| A、1-ln 2 | ||
B、
| ||
| C、1+ln 2 | ||
D、
|
考点:利用导数研究曲线上某点切线方程,反函数
专题:函数的性质及应用
分析:首先,根据互为反函数的两个函数的图象之间的关系,得到:两曲线上点之间的最小距离就是y=x与y=
ex上点的最小距离的2倍.然后,利用导数在函数y=
ex上求解切点,使得它与直线y=x平行,最后借助于点到直线的距离公式,求解最小距离.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:由题意知函数y=
ex与y=ln(2x)互为反函数,
其图象关于直线y=x对称,
两曲线上点之间的最小距离就是y=x与y=
ex上点的最小距离的2倍.
设y=
ex上点(x0,y0)处的切线与直线y=x平行,
则
ex0=1,
∴x0=ln 2,y0=1,
∴点(x0,y0)到y=x的距离为
=
(1-ln 2),
则|PQ|的最小值为
(1-ln 2)×2=
(1-ln 2).
故选:B.
| 1 |
| 2 |
其图象关于直线y=x对称,
两曲线上点之间的最小距离就是y=x与y=
| 1 |
| 2 |
设y=
| 1 |
| 2 |
则
| 1 |
| 2 |
∴x0=ln 2,y0=1,
∴点(x0,y0)到y=x的距离为
| |ln2-1| | ||
|
| ||
| 2 |
则|PQ|的最小值为
| ||
| 2 |
| 2 |
故选:B.
点评:本题综合考查了互为反函数的图象之间的关系,导数的几何意义等知识,属于综合性题目,难度中等.

练习册系列答案
相关题目
下列对零点说法正确的有几个( )
①函数y=f(x)的零点就是方程y=f(x)的根;
②函数y=f(x)的零点就是y=f(x)的图象与x轴的交点;
③函数y=f(x)的零点就是实数;
④函数y=f(x)的零点是平面上的一个点.
①函数y=f(x)的零点就是方程y=f(x)的根;
②函数y=f(x)的零点就是y=f(x)的图象与x轴的交点;
③函数y=f(x)的零点就是实数;
④函数y=f(x)的零点是平面上的一个点.
| A、1个 | B、2个 | C、3个 | D、4个 |
复数
在复平面内对应的点位于( )
| 1-i |
| 2+3i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
i是虚数单位,复数(
)2表示的点落在哪个象限( )
| 3-i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知l,m,n是空间三条不同直线,命题p:若l⊥m,l⊥n,则m∥n;命题q:若三条直线l,m,n两两相交,则直线l,m,n共面,则下列命题为真命题的是( )
| A、p∧q | B、p∨q |
| C、p∨(¬q) | D、(¬p)∧q |
已知n∈N,常数p,q均大于1,且都不等于2,则
=( )
| lim |
| n→∞ |
| pn+1-qn |
| pn+2-2qn+1 |
A、
| ||||||
B、-
| ||||||
C、
| ||||||
D、-
|
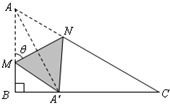 如图,直角三角形ABC中,∠B=90°,AB=1,BC=
如图,直角三角形ABC中,∠B=90°,AB=1,BC=