Question

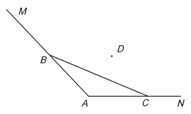在一个六角形体育馆的一角MAN内，用长为a的围栏设置一个运动器材储存区域（如图所示），已知∠A=120°，B是墙角线AM上的一点，C是墙角线AN上的一点．
（1）若BC=a=20，求储存区域面积的最大值；
（2）若AB=AC=10，在折线MBCN内选一点D，使BD+DC=20，求四边形储存区域DBAC的最大面积．

Answer 1

考点：解三角形的实际应用

专题：应用题,解三角形

分析：（1）设AC=x，AB=y，（x，y为正数），由余弦定理，结合三角形的面积公式，利用基本不等式可得储存区域面积的最大值；
（（2）只考虑三角形BCD的面积变化，点D的轨迹是一个椭圆，B、C是其焦点，结合椭圆的知识得结果．

解答： 解：（1）设AB=x，AC=y，x＞0，y＞0．
由20²=x²+y²-2xycos120°≥2xy-2xycos120°，
得xy≤

202

2-2cos120°

=

202

4sin260°

．
∴S=

1

2

xysin120°≤

1

2

•

202

4sin260°

•2sin60°cos60°=

202cos60°

4sin60°

=

202

4tan60°

=

100 3

3

．
即四边形DBAC面积的最大值为

100 3

3

，当且仅当x=y时取到．
（2）由DB+DC=20，知点D在以B，C为焦点的椭圆上，
∵S△ABC=

1

2

×10×10×

3

2

=25

3

，
∴要使四边形DBAC面积最大，只需△DBC的面积最大，此时点D到BC的距离最大，即D必为椭圆短轴顶点．
由BC=10

3

，得短半轴长b=5，S_△BCD面积的最大值为

1

2

×10

3

×5=25

3

．
因此，四边形ACDB面积的最大值为50

3

．

点评：本题为基本不等式和椭圆知识的结合，数列掌握基本不等式和椭圆的定义是解决问题关键，属中档题．