题目内容
 如图,圆O为三棱锥P-ABC的底面ABC的外接圆,AC是圆O的直径,PA⊥BC,点M是线段PA的中点.
如图,圆O为三棱锥P-ABC的底面ABC的外接圆,AC是圆O的直径,PA⊥BC,点M是线段PA的中点.(1)求证:BC⊥PB;
(2)设PA⊥AC,PA=AC=2,AB=1,求三棱锥P-MBC的体积;
(3)在△ABC内是否存在点N,使得MN∥平面PBC?请证明你的结论.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)由已知得BC⊥AB,BC⊥平面PAB,由此能证明BC⊥PB.
(2)由已知得BC=
,S△ABC=
,PA⊥平面ABC,由此能求出三棱锥P-MBC的体积.
(3)取AB的中点D,连结OD、MD、OM,则N为线段OD(除端点O,D外)任意一点即可使得MN∥平面PBC.由已知得MD∥PB,MO∥PC,从而平面MDO∥平面PBC,由此能证明MN∥平面PBC.
(2)由已知得BC=
| 3 |
| ||
| 2 |
(3)取AB的中点D,连结OD、MD、OM,则N为线段OD(除端点O,D外)任意一点即可使得MN∥平面PBC.由已知得MD∥PB,MO∥PC,从而平面MDO∥平面PBC,由此能证明MN∥平面PBC.
解答:
(1)证明:如图,∵AC是圆O的直径,∴BC⊥AB,
∵BC⊥PA,又PA、AB?平面PAB,且PA∩AB=A,
∴BC⊥平面PAB,又PB?平面PAB,
∴BC⊥PB.
(2)解:如图,在Rt△ABC中,AC=2,AB=1,
∴BC=
,∴S△ABC=
,
∵PA⊥BC,PA⊥AC,∴PA⊥平面ABC,
∴VP-MBC=VP-ABC-VM-ABC
=
×
×2-
×
×1=
.
(3)解:如图,取AB的中点D,连结OD、MD、OM,
则N为线段OD(除端点O,D外)任意一点即可使得MN∥平面PBC.
理由如下:
∵M、O、D分别是PA、AC、AB的中点,
∴MD∥PB,MO∥PC,
∵MD?平面PBC,PB?平面PBC,∴MD∥平面PBC,
同理,得MO∥平面PBC,
∵MD、MO?平面MDO,MD∩MO=M,
∴平面MDO∥平面PBC,
∵MN?平面MDO,∴MN∥平面PBC.

∵BC⊥PA,又PA、AB?平面PAB,且PA∩AB=A,
∴BC⊥平面PAB,又PB?平面PAB,
∴BC⊥PB.
(2)解:如图,在Rt△ABC中,AC=2,AB=1,
∴BC=
| 3 |
| ||
| 2 |
∵PA⊥BC,PA⊥AC,∴PA⊥平面ABC,
∴VP-MBC=VP-ABC-VM-ABC
=
| 1 |
| 3 |
| ||
| 2 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 6 |
(3)解:如图,取AB的中点D,连结OD、MD、OM,
则N为线段OD(除端点O,D外)任意一点即可使得MN∥平面PBC.
理由如下:
∵M、O、D分别是PA、AC、AB的中点,
∴MD∥PB,MO∥PC,
∵MD?平面PBC,PB?平面PBC,∴MD∥平面PBC,
同理,得MO∥平面PBC,
∵MD、MO?平面MDO,MD∩MO=M,
∴平面MDO∥平面PBC,
∵MN?平面MDO,∴MN∥平面PBC.
点评:本题考查异面直线竽的证明,考查三棱锥的体积的求法,考查在△ABC内是否存在点N,使得MN∥平面PBC的判断与证明,解题时要注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=ax3+bx2+cx+d的图象如图所示,其导函数是f′(x),则
=( )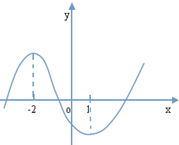
| f′(3) |
| f′(-1) |

| A、-2 | B、2 | C、5 | D、-5 |