题目内容
等边三角形ABC的边长为a,AD是BC边上的高,沿AD将△ABC折成直二面角,则点A到BC的距离为 .
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:利用二面角确定∠BDC=90°,过D作DO垂直于BC于O,所以O是BC的中点,连接AO,证明AO即为点A到BC的距离,即可求出结论.
解答:
解:如图,因为AD是正△ABC的高线,所以∠BDC即为二面角的平面角,即∠BDC=90°,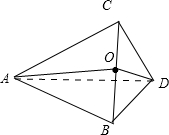
过D作DO垂直于BC于O,所以O是BC的中点,连接AO.等边三角形ABC的边长为a,
因为CD=BD=
,所以BC=
,所以DO=
因为AD⊥底面BDC,所以AD⊥BC,
又因为DO⊥BC,并且AD∩DO=D,
所以BC⊥面ADO,所以BC⊥AO,即AO即为点A到BC的距离
∴A0=
=
故答案为:
.

过D作DO垂直于BC于O,所以O是BC的中点,连接AO.等边三角形ABC的边长为a,
因为CD=BD=
| a |
| 2 |
| ||
| 2 |
| ||
| 4 |
因为AD⊥底面BDC,所以AD⊥BC,
又因为DO⊥BC,并且AD∩DO=D,
所以BC⊥面ADO,所以BC⊥AO,即AO即为点A到BC的距离
∴A0=
(
|
| ||
| 4 |
故答案为:
| ||
| 4 |
点评:本题考查面面角,考查空间距离的计算,属于中档题.

练习册系列答案
相关题目
命题“?x>1,log2x>0”的否定形式是( )
| A、?x0>1,log2x≤0 |
| B、?x0≤1,log2x≤0 |
| C、?x>1,log2x≤0 |
| D、?x≤1,log2x>0 |
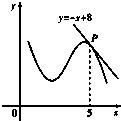 如图,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=( )
如图,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=( )| A、2 | ||
| B、1 | ||
C、
| ||
| D、0 |
 如图,圆O为三棱锥P-ABC的底面ABC的外接圆,AC是圆O的直径,PA⊥BC,点M是线段PA的中点.
如图,圆O为三棱锥P-ABC的底面ABC的外接圆,AC是圆O的直径,PA⊥BC,点M是线段PA的中点.