题目内容

证明等式（1-tan4A）cos2A+tan2A=1成立．
考点：三角函数恒等式的证明
专题：推理和证明
分析：将所证关系式的左端转化为：左端=（1-tan2A）•
cos2A+sin2A
cos2A
•cos2A+tan2A，整理即得右端．
解答： 证明：左端=（1-tan4A）cos2A+tan2A
=（1-tan2A）（1+tan2A）cos2A+tan2A
=（1-tan2A）•
cos2A+sin2A
cos2A
•cos2A+tan2A
=1-tan2A+tan2A=1=右端．
故等式成立．
点评：本题考查三角函数恒等式的证明，考查转化思想与推理证明能力，属于中档题．
练习册系列答案
相关题目
如图，圆O为三棱锥P-ABC的底面ABC的外接圆，AC是圆O的直径，PA⊥BC，点M是线段PA的中点．
（1）求证：BC⊥PB；
（2）设PA⊥AC，PA=AC=2，AB=1，求三棱锥P-MBC的体积；
（3）在△ABC内是否存在点N，使得MN∥平面PBC？请证明你的结论．
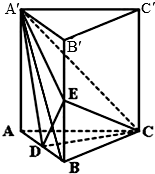如图，直三棱柱ABC-A′B′C′中，AC=BC=5，AA′=AB=6，D、E分别为AB和BB′上的点，且
AD
DB
=
BE
EB′
=λ．
（1）求证：当λ=1时，A′B⊥CE；
（2）当λ为何值时，三棱锥A′-CDE的体积最小，并求出最小体积．
抛掷两个骰子，至少有一个3点或6点出现时，就说这次试验成功，则在81次试验中，成功次数ξ的方差是
 
．
已知函数f（x）=sin
π
2
x，任取t∈R，记函数f（x）在区间[t，t+1]上的最大值为Mt，最小值为mt，h（t）=Mt-mt，则函数h（t）的值域为
 
．
下列命题中，真命题的序号是
 

①△ABC中，A＞B?sinA＞sinB
②数列{an}的前n项和Sn=n2-2n+1，则数列{an}是等差数列．
③锐角三角形的三边长分别为3，4，a，则a的取值范围是
7
＜a＜5．
④等差数列{an}前n项和为Sn，已知am-1+am+1-am2=0，S2m-1=38，则m=10．
若方程mx2+（m-4）y2=1表示双曲线，则m的取值范围为（　　）
A、0＜m＜4B、m＞0
C、m＜4D、m＞4
从1，2，3，…，16中任取四个不同的数，求其中至少有两个是相邻数的概率．
已知函数y=2sin（
1
2
x+φ）（0＜φ＜π），图象的一条对称轴是直线x=
2π
3
．
（Ⅰ）求φ；
（Ⅱ）写出由y=sinx图象变换到y=2sin（
1
2
x+φ）图象的过程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网