题目内容

已知矩形ABCD的顶点都在半径为2的球O的球面上，且AB=3，BC=
3
，DE垂直于平面ABCD，交球O于E，则棱锥E-ABCD的体积为
 
．
考点：棱柱、棱锥、棱台的体积
专题：空间位置关系与距离
分析：由已知得BE过球心，从而DE=
42-32-(
3
)2
=2，由此能求出棱锥E-ABCD的体积．
解答： 解：如图所示，BE过球心，
∴DE=
42-32-(
3
)2
=2，
∴VE-ABCD=
1
3
×3×
3
×2=2
3
．
故答案为：2
3
．
点评：本题考查棱锥的体积的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
若点A（-2，1），B（1，3），则
AB
=
 
．
已知向量
a
=（cosα，-1），
b
=（2，1+sinα），且
a
•
b
=-1．
（1）求tanα的值；
（2）求
2sinα-3cosα
4sinα-9cosα
的值．
要使
x2-2x
有意义，x的取值应为
 
．
已知f（x）定义域为[1，2]，y=f（2x+
1
4
）+f（2x-
1
4
）的定义域为
 
．
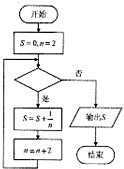阅读如图所示的程序框图，运行相应的程序，若输出的S为
11
12
，则判断框中填写的内容可以是（　　）
A、n=6B、n＜6
C、n≤6D、n≤8
如图，圆O为三棱锥P-ABC的底面ABC的外接圆，AC是圆O的直径，PA⊥BC，点M是线段PA的中点．
（1）求证：BC⊥PB；
（2）设PA⊥AC，PA=AC=2，AB=1，求三棱锥P-MBC的体积；
（3）在△ABC内是否存在点N，使得MN∥平面PBC？请证明你的结论．
一个正方体的对角线长为l，那么这个正方体的全面积为（　　）
A、2
2
l2
B、2l2
C、2
3
l2
D、3
2
l2
抛掷两个骰子，至少有一个3点或6点出现时，就说这次试验成功，则在81次试验中，成功次数ξ的方差是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网