题目内容

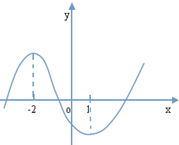
已知函数f（x）=ax3+bx2+cx+d的图象如图所示，其导函数是f′（x），则
f′(3)
f′(-1)
=（　　）
A、-2B、2C、5D、-5
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：求导数，结合图象可得f′（-2）=f′（1）=0，用c表示出a和b，代入要求的式子把a，b代入可得关于c的式子的比值，可约去c，即可的答案．
解答： 解：求导得：f′（x）=3ax2+2bx+c，结合图象可得
x=-2，1为导函数的零点，即f′（-2）=f′（1）=0，
∴
12a-4b+c=0
3a+2b+c=0
，解得：
a=-
c
6
b=-
c
4
，
∴
f′(3)
f′(-1)
=
27a+6b+c
3a-2b+c
=-5，
故选：D．
点评：本题为导数和图象的关系，用c表示a，b是解决问题的关键，属基础题．
练习册系列答案
相关题目
设偶函数f（x）的定义域为R，当x∈[0，+∞）时f（x）是增函数，则f（-2），f（π），f（-3）的大小关系是（　　）
A、f（π）＜f（-2）＜f（-3）
B、f（π）＜f（-3）＜f（-2）
C、f（π）＞f（-2）＞f（-3）
D、f（π）＞f（-3）＞f（-2）
已知f（x）定义域为[1，2]，y=f（2x+
1
4
）+f（2x-
1
4
）的定义域为
 
．
如图，圆O为三棱锥P-ABC的底面ABC的外接圆，AC是圆O的直径，PA⊥BC，点M是线段PA的中点．
（1）求证：BC⊥PB；
（2）设PA⊥AC，PA=AC=2，AB=1，求三棱锥P-MBC的体积；
（3）在△ABC内是否存在点N，使得MN∥平面PBC？请证明你的结论．
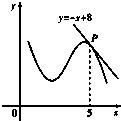如图，函数y=f（x）的图象在点P处的切线方程是y=-x+8，则f（5）+f′（5）=（　　）
A、2
B、1
C、
1
2
D、0
一个正方体的对角线长为l，那么这个正方体的全面积为（　　）
A、2
2
l2
B、2l2
C、2
3
l2
D、3
2
l2
过点P（1，2）的直线l与圆C：（x+3）2+（y-4）2=36交于A、B两点，当|AB|最小时，直线l的方程是
 
．
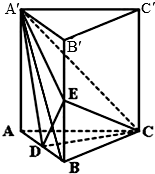如图，直三棱柱ABC-A′B′C′中，AC=BC=5，AA′=AB=6，D、E分别为AB和BB′上的点，且
AD
DB
=
BE
EB′
=λ．
（1）求证：当λ=1时，A′B⊥CE；
（2）当λ为何值时，三棱锥A′-CDE的体积最小，并求出最小体积．
若方程mx2+（m-4）y2=1表示双曲线，则m的取值范围为（　　）
A、0＜m＜4B、m＞0
C、m＜4D、m＞4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网