题目内容
数列{an}中,已知a1=2,对n∈N*,恒有an•an+1=2×4n成立.
(1)求证:数列{an}是等比数列;
(2)设bn=a6n-5+a6n-3+a6n-1,求数列{bn}前n项和Sn.
(1)求证:数列{an}是等比数列;
(2)设bn=a6n-5+a6n-3+a6n-1,求数列{bn}前n项和Sn.
考点:数列的求和,等比关系的确定
专题:等差数列与等比数列
分析:(1)由递推公式,求出{an}的通项公式,从而证明等比数列;
(2)由等比数列前n项和公式,求出Sn.
(2)由等比数列前n项和公式,求出Sn.
解答:
解:(1)证明:a1=2,又a1•a2=2×4=8,得a2=4,
∵an•an+1=2×4n,∴an+1•an+2=2×4n+1,
两式相除得
=4,知数列{an}奇数项成等比,首项a1=2,公比q=4,
∴n为奇数时,an=a1×4
=2n,
当 n为奇数时,则n+1为偶数,由an•an+1=2×4n得2n•an+1=2×4n,an+1=2n+1,
∴对n∈N*,恒有an=2n,
=
=2(定值),故数列{an}是等比数列;
(2)Sn=b1+b2+…+bn=(a1+a3+a5)+(a7+a9+a11)+…+(a6n-5+a6n-3+a6n-1),
数列{bn}前n项和Sn即是数列{an}奇数项和(共3n项),
则Sn=
=
(26n-1).
∵an•an+1=2×4n,∴an+1•an+2=2×4n+1,
两式相除得
| an+2 |
| an |
∴n为奇数时,an=a1×4
| n-1 |
| 2 |
当 n为奇数时,则n+1为偶数,由an•an+1=2×4n得2n•an+1=2×4n,an+1=2n+1,
∴对n∈N*,恒有an=2n,
| an+1 |
| an |
| 2n+1 |
| 2n |
(2)Sn=b1+b2+…+bn=(a1+a3+a5)+(a7+a9+a11)+…+(a6n-5+a6n-3+a6n-1),
数列{bn}前n项和Sn即是数列{an}奇数项和(共3n项),
则Sn=
| 2(1-43n) |
| 1-4 |
| 2 |
| 3 |
点评:由递推公式求通项公式,需要根据递推公式的特点,进行适当变形,还考查了等比数列的前n项和公式,这些都是常考题.属于中档题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
复数z=-2+i,则它的共轭复数
在复平面内对应的点位于( )
. |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
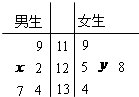 某数学兴趣小组有男女生各5名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为125,女生数据的平均数为126.8.
某数学兴趣小组有男女生各5名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为125,女生数据的平均数为126.8.