题目内容
已知f(x)=sinx(cosx-sinx),x∈R.
(1)求f(x)的最大值和单调增区间;
(2)若a∈(0,
),f(a)=
,求a的值.
(1)求f(x)的最大值和单调增区间;
(2)若a∈(0,
| π |
| 2 |
| ||
| 4 |
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:三角函数的图像与性质
分析:(1)利用三角函数的倍角公式将函数进行化简即可求f(x)的最大值和单调增区间;
(2)若a∈(0,
),求出f(a)=
,得sin(2α+
)=
,解方程即可求a的值.
(2)若a∈(0,
| π |
| 2 |
| ||
| 4 |
| π |
| 4 |
| 1 |
| 2 |
解答:
解:(1)f(x)=sinx(cosx-sinx)=sinxcosx-sin2x)=
sin2x-
=
sin2x+
cos2x-
=
sin(2x+
)-
,
当sin(2x+
)=1时,函数f(x)取得最大值,即f(x)的最大值为
-
,
由2kπ-
≤2x+
≤2kπ+
,k∈Z,
解得kπ-
≤x≤kπ+
,
即函数的单调增区间为[kπ-
,kπ+
],k∈Z;
(2)f(a)=
sin(2α+
)-
=
,
即sin(2α+
)=
,
若a∈(0,
),则2α+
∈(
,
),
∴2α+
=
,解得α=
.
| 1 |
| 2 |
| 1-cos2x |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
当sin(2x+
| π |
| 4 |
| ||
| 2 |
| 1 |
| 2 |
由2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
解得kπ-
| 3π |
| 8 |
| π |
| 8 |
即函数的单调增区间为[kπ-
| 3π |
| 8 |
| π |
| 8 |
(2)f(a)=
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| ||
| 4 |
即sin(2α+
| π |
| 4 |
| 1 |
| 2 |
若a∈(0,
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
∴2α+
| π |
| 4 |
| 5π |
| 6 |
| 7π |
| 24 |
点评:本题主要考查三角函数的最值和单调区间的求解,根据倍角公式将函数化简是解决本题的关键,要求熟练三角函数的图象和性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
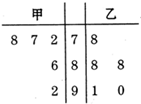 甲、乙两位同学在高二5次月考的数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是
甲、乙两位同学在高二5次月考的数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是. |
| x甲 |
. |
| x乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
从2014年到2017年期间,甲计划每年6月6日都到银行存入a元的一个定期储蓄,若年利率q保持不变,且每年到期的存款本息均自动转为新的一年定期储蓄,若到2017年6月6日,甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )元.
| A、a(1+q)3 | ||
| B、a(1+q)5 | ||
C、
| ||
D、
|
若方程ln(x+1)+2x-1=0的根为x=m,则( )
| A、0<m<1 |
| B、1<m<2 |
| C、2<m<3 |
| D、3<m<4 |
 将各项均为正数的数列{an}排成如图所示的三角形数阵(第n行有n个数,同一行下标小的排在左边).bn表示数阵中第n行第1列的数.
将各项均为正数的数列{an}排成如图所示的三角形数阵(第n行有n个数,同一行下标小的排在左边).bn表示数阵中第n行第1列的数.