题目内容
从2014年到2017年期间,甲计划每年6月6日都到银行存入a元的一个定期储蓄,若年利率q保持不变,且每年到期的存款本息均自动转为新的一年定期储蓄,若到2017年6月6日,甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )元.
| A、a(1+q)3 | ||
| B、a(1+q)5 | ||
C、
| ||
D、
|
考点:等比数列的前n项和
专题:等差数列与等比数列
分析:先分别计算每一年存入a元到2017年的本息和,然后将所有存款的本息相加,由等比数列求得求和公式可得.
解答:
解:2014年的a元到了2017年本息和为a(1+q)3,
2015年的a元到了2017年本息和为a(1+q)2,
2016年的a元到了2017年本息和为a(1+q),
所有金额为a(1+q)+a(1+q)2+a(1+q)3
即所有金额为
=
故选:C
2015年的a元到了2017年本息和为a(1+q)2,
2016年的a元到了2017年本息和为a(1+q),
所有金额为a(1+q)+a(1+q)2+a(1+q)3
即所有金额为
| a(1+q)[1-(1+q)3] |
| 1-(1+q) |
| a[(1+q)4-(1+q)] |
| q |
故选:C
点评:本题考查等比数列,涉及数列的应用和等比数列的求和公式,属中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
下列各组向量不平行的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图是2012年举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和中位数分别为( )
如图是2012年举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和中位数分别为( )| A、85,84 |
| B、85,84.5 |
| C、85,85 |
| D、85,85.5 |
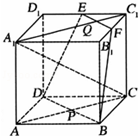 如图:在正方体ABCD-A1B1C1D1中,E,F分别为D1C1,B1C1的中点,AC∩BD=P,A1C1∩EF=Q;
如图:在正方体ABCD-A1B1C1D1中,E,F分别为D1C1,B1C1的中点,AC∩BD=P,A1C1∩EF=Q;