题目内容
 将各项均为正数的数列{an}排成如图所示的三角形数阵(第n行有n个数,同一行下标小的排在左边).bn表示数阵中第n行第1列的数.
将各项均为正数的数列{an}排成如图所示的三角形数阵(第n行有n个数,同一行下标小的排在左边).bn表示数阵中第n行第1列的数.已知数列{bn}为等比数列,且从第3行开始,各行均构成公差为d的等差数列,a1=1,a12=17,a18=34.
(1)求数阵中第m行第n列(m,n∈N+且m≥3,n≤m)的数Amn(用m,n表示);
(2)试问a2015处在数阵中第几行第几列?
(3)试问这个数列中是否有2015这个数?有求出具体位置,没有说明理由.
考点:等差数列与等比数列的综合
专题:等差数列与等比数列
分析:(1)由题意和等差、等比数列的通项公式,列出关于公差d和公比q的方程组,求出q、d的值、bn,由题意和等差、等比数列的通项公式求出Amn的表达式;
(2)由图表得到每一行中数的个数,由等差数列的求和公式求出前62、63行数的个数,从而确定a2015为数阵中第63行第62列的数;
(3)假设2015为数阵中第m行第n列的数,由数的规律列出不等式,再取特值进行验证,从而确定不等式没有整数解,即可说明2015不在该数阵中.
(2)由图表得到每一行中数的个数,由等差数列的求和公式求出前62、63行数的个数,从而确定a2015为数阵中第63行第62列的数;
(3)假设2015为数阵中第m行第n列的数,由数的规律列出不等式,再取特值进行验证,从而确定不等式没有整数解,即可说明2015不在该数阵中.
解答:
解:(1)设公比为q,公差为d,
由题意知:a1=1,a12=17,a18=34,
所以b1=a1=1,则
,…2分
解得:q=2、d=1,则bn=2n-1,
所以Amn=bm+(n-1)d=2n-1+n-1…4分
(2)由表格知:每一行中有n个数,
因为1+2+3+…+62=
=1953,1+2+3+…+63=1953+63=2016…6分
所以2015-1953=62…8分
则a2015为数阵中第63行第62列的数.…10分
(3)假设2015为数阵中第m行第n列的数,
由第m行最小的数为2m-1,最大的数为2m-1+m-1,
所以2m-1≤2015≤2m-1+m-1,…14分
当m≤11时,2m-1+m-1≤210+10=1034<2013;…16分
当m≥12时,2m-1≥211=2048>2015,
于是,不等式2m-1≤2015≤2m-1+m-1没有整数解,
所以2015不在该数阵中.…18分.
由题意知:a1=1,a12=17,a18=34,
所以b1=a1=1,则
|
解得:q=2、d=1,则bn=2n-1,
所以Amn=bm+(n-1)d=2n-1+n-1…4分
(2)由表格知:每一行中有n个数,
因为1+2+3+…+62=
| 62(1+62) |
| 2 |
所以2015-1953=62…8分
则a2015为数阵中第63行第62列的数.…10分
(3)假设2015为数阵中第m行第n列的数,
由第m行最小的数为2m-1,最大的数为2m-1+m-1,
所以2m-1≤2015≤2m-1+m-1,…14分
当m≤11时,2m-1+m-1≤210+10=1034<2013;…16分
当m≥12时,2m-1≥211=2048>2015,
于是,不等式2m-1≤2015≤2m-1+m-1没有整数解,
所以2015不在该数阵中.…18分.
点评:本题考查等差、等比数列的通项公式,归纳法的应用,考查综合分析问题和解决问题的能力,解答此题要有很好的耐心,考查了逻辑思维能力和运算能力,是难度非常大的少见题目.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
已知x>0,y>0,x+
=4,则
+y的最小值为( )
| 1 |
| y |
| 1 |
| x |
| A、4 | ||
B、
| ||
C、
| ||
| D、1 |
设F1,F2是双曲线x2-y2=a2的两个焦点,Q是双曲线上任意一点,从F1引∠F1QF2平分线的垂线,垂足是P,则点P的轨迹是( )
| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |
下列各组向量不平行的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
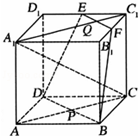 如图:在正方体ABCD-A1B1C1D1中,E,F分别为D1C1,B1C1的中点,AC∩BD=P,A1C1∩EF=Q;
如图:在正方体ABCD-A1B1C1D1中,E,F分别为D1C1,B1C1的中点,AC∩BD=P,A1C1∩EF=Q;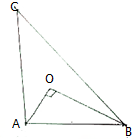 如图所示,已知点O为△ABC的重心,OA⊥OB,AB=6,则
如图所示,已知点O为△ABC的重心,OA⊥OB,AB=6,则