题目内容
已知函数f(x)=|x-1|
(Ⅰ)解不等式f(2x)+f(x+4)≥8;
(Ⅱ)若|a|<1,|b|<1,a≠0,求证:
>f(
).
(Ⅰ)解不等式f(2x)+f(x+4)≥8;
(Ⅱ)若|a|<1,|b|<1,a≠0,求证:
| f(ab) |
| |a| |
| b |
| a |
考点:绝对值不等式的解法
专题:不等式的解法及应用,推理和证明
分析:(Ⅰ)依题意,f(2x)+f(x+4)=|2x-1|+|x+3|=
,利用分段函数分段解不等式f(2x)+f(x+4)≥8,即可求得其解集.
(Ⅱ)|a|<1,|b|<1,
>f(
)?f(ab)>|a|f(
)?|ab-1|>|a-b|,要证该不等式成立,只需证明|ab-1|2-|a-b|2>0即可.
|
(Ⅱ)|a|<1,|b|<1,
| f(ab) |
| |a| |
| b |
| a |
| b |
| a |
解答:
(Ⅰ)解:f(2x)+f(x+4)=|2x-1|+|x+3|=
,
当x<-3时,由-3x-2≥8,解得x≤-
;
当-3≤x<
时,由-x+4≥8,解得x∈∅;
当x≥
时,由3x+2≥8,解得x≥2…4分
所以,不等式f(2x)+f(x+4)≥8的解集为{x|x≤-
或x≥2}…5分;
(Ⅱ)证明:
>f(
)等价于f(ab)>|a|f(
),即|ab-1|>|a-b|,
因为|a|<1,|b|<1,
所以|ab-1|2-|a-b|2=(a2b2-2ab+1)-(a2-2ab+b2)=(a2-1)(b2-1)>0,
所以,|ab-1|>|a-b|,故所证不等式成立…10分.
|
当x<-3时,由-3x-2≥8,解得x≤-
| 10 |
| 3 |
当-3≤x<
| 1 |
| 2 |
当x≥
| 1 |
| 2 |
所以,不等式f(2x)+f(x+4)≥8的解集为{x|x≤-
| 10 |
| 3 |
(Ⅱ)证明:
| f(ab) |
| |a| |
| b |
| a |
| b |
| a |
因为|a|<1,|b|<1,
所以|ab-1|2-|a-b|2=(a2b2-2ab+1)-(a2-2ab+b2)=(a2-1)(b2-1)>0,
所以,|ab-1|>|a-b|,故所证不等式成立…10分.
点评:本题考查绝对值不等式的解法,着重考查分类讨论思想与等价转化思想的综合运用,考运算及推理、证明能力,属于中档题.

练习册系列答案
相关题目
已知复数z的共轭复数是
,则复数z3+2z2+
+1等于( )
| 2-2i |
| 1+i |
. |
| z |
| A、8+2i | B、5+3i |
| C、-7-10i | D、9-10i |
下列各组向量不平行的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图是2012年举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和中位数分别为( )
如图是2012年举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和中位数分别为( )| A、85,84 |
| B、85,84.5 |
| C、85,85 |
| D、85,85.5 |
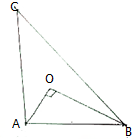 如图所示,已知点O为△ABC的重心,OA⊥OB,AB=6,则
如图所示,已知点O为△ABC的重心,OA⊥OB,AB=6,则