题目内容
6.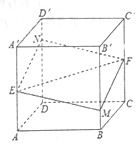 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱是AA′,CC′的中点,过直线EF的平面分别与棱BB′,DD′交于M,N,设BM=x,x∈[0,1],给出以下四种说法:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱是AA′,CC′的中点,过直线EF的平面分别与棱BB′,DD′交于M,N,设BM=x,x∈[0,1],给出以下四种说法:(1)平面MENF⊥平面BDD′B′;
(2)当且仅当x=$\frac{1}{2}$时,四边形MENF的面积最小;
(3)四边形MENF周长L=f(x),x∈[0,1]是单调函数;
(4)四棱锥C′-MENF的体积V=h(x)为常函数,以上说法中正确的为( )
| A. | (2)(3) | B. | (1)(3)(4) | C. | (1)(2)(3) | D. | (1)(2) |
分析 (1)利用面面垂直的判定定理去证明EF⊥平面BDD′B′.(2)四边形MENF的对角线EF是固定的,所以要使面积最小,则只需MN的长度最小即可.(3)判断周长的变化情况.(4)求出四棱锥的体积,进行判断.
解答  解:(1)连结BD,B′D′,则由正方体的性质可知,EF⊥平面BDD′B′,所以平面MENF⊥平面BDD′B′,所以正确.
解:(1)连结BD,B′D′,则由正方体的性质可知,EF⊥平面BDD′B′,所以平面MENF⊥平面BDD′B′,所以正确.
(2)连结MN,因为EF⊥平面BDD′B′,所以EF⊥MN,四边形MENF的对角线EF是固定的,所以要使面积最小,则只需MN的长度最小即可,此时当M为棱的中点时,即x=$\frac{1}{2}$时,此时MN长度最小,对应四边形MENF的面积最小.所以正确.
(3)因为EF⊥MN,所以四边形MENF是菱形.当x∈[0,$\frac{1}{2}$]时,EM的长度由大变小.当x∈[$\frac{1}{2}$,1]时,EM的长度由小变大.所以函数L=f(x)不单调.所以错误.
(4)连结C′E,C′M,C′N,则四棱锥则分割为两个小三棱锥,它们以C′EF为底,以M,N分别为顶点的两个小棱锥.因为三角形C′EF的面积是个常数.M,N到平面C'EF的距离是个常数,所以四棱锥C'-MENF的体积V=h(x)为常函数,所以正确.
故选C.
点评 本题考查空间立体几何中的面面垂直关系以及空间几何体的体积公式,本题巧妙的把立体几何问题和函数进行的有机的结合,综合性较强,设计巧妙,对学生的解题能力要求较高.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.设f(x)是定义在R上的偶函数,f(x)=-f(x+1),当x∈[0,1]时,f(x)=x+2,则当x∈[-2,0]时,f(x)=( )
| A. | f(x)=x+4 | B. | f(x)=2+|x+1| | C. | f(x)=2-x | D. | f(x)=3-|x+1| |
18.已知抛物线x2=2py(p>0)的焦点为F,过点F且倾斜角为150°的直线l与抛物线在第一、二象限分别交于A,B两点,则$\frac{{|{BF}|}}{{|{AF}|}}$等于( )
| A. | 3 | B. | $7+4\sqrt{3}$ | C. | $\frac{1}{3}$ | D. | $3+2\sqrt{2}$ |
15.下列函数中,是奇函数且在(0,+∞)上单调递减的是( )
| A. | y=x-1 | B. | y=($\frac{1}{2}$)x | C. | y=x3 | D. | $y={log_{\frac{1}{2}}}x$ |
16.函数$f(x)=lnx-\frac{2}{x}$的零点所在的大致区间是( )
| A. | (e,+∞) | B. | $(\frac{1}{e},1)$ | C. | (2,3) | D. | (e,+∞) |
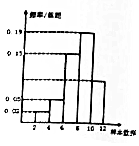 有一个容量为200的样本,其频率分布直方图如图所示,根据样本的频率分布直方图估计,样本数据落在区间[10,12]内的频数为36.
有一个容量为200的样本,其频率分布直方图如图所示,根据样本的频率分布直方图估计,样本数据落在区间[10,12]内的频数为36.