题目内容
1.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),离心率为$\frac{\sqrt{3}}{2}$,两焦点分别为F1、F2,过F1的直线交椭圆C于M、N两点,且△MF2N的周长为8.(Ⅰ)求椭圆C的方程;
(Ⅱ)若|MN|=$\frac{8}{5}$,求△MF2N的面积.
分析 (Ⅰ)利用已知条件求出椭圆方程中的几何量,即可求椭圆C的方程;
(Ⅱ)设直线MN的方程为x=ty-$\sqrt{3}$,联立直线方程与椭圆方程,化为关于y的一元二次方程,由弦长求得t值,然后代入三角形面积公式求得△MF2N的面积.
解答 解:(Ⅰ)由题得:$\frac{c}{a}=\frac{\sqrt{3}}{2}$,4a=8,∴a=2,c=$\sqrt{3}$.
又b2=a2-c2=1,
∴椭圆C的方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(Ⅱ)设直线MN的方程为x=ty-$\sqrt{3}$,
联立$\left\{\begin{array}{l}{x=ty-\sqrt{3}}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,得$({t}^{2}+4){y}^{2}-2\sqrt{3}ty-1=0$.
设M、N的坐标分别为(x1,y1),(x2,y2),
则${y}_{1}+{y}_{2}=\frac{2\sqrt{3}t}{{t}^{2}+4}$,${y}_{1}{y}_{2}=\frac{-1}{{t}^{2}+4}$,
|MN|=$\sqrt{1+{t}^{2}}|{y}_{1}-{y}_{2}|$=$\sqrt{1+{t}^{2}}\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$
=$\sqrt{1+{t}^{2}}\sqrt{(\frac{2\sqrt{3}t}{{t}^{2}+4})^{2}+\frac{4}{{t}^{2}+4}}$=$\frac{8}{5}$,解得:t2=1.
∴${S}_{△M{F}_{2}N}$=$\frac{1}{2}•2c•|{y}_{1}-{y}_{2}|$=$\sqrt{3}•$$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$
=$\sqrt{3}•\sqrt{(\frac{2\sqrt{3}t}{{t}^{2}+4})^{2}+\frac{4}{{t}^{2}+4}}$=$\sqrt{3}•\sqrt{\frac{12}{25}+\frac{4}{5}}=\frac{4\sqrt{6}}{5}$.
点评 本题考查椭圆的方程的求法,直线与椭圆的位置关系,弦长公式的应用,考查分析问题解决问题的能力以及转化思想的应用,是中档题.

 名校课堂系列答案
名校课堂系列答案| A. | 2 | B. | 1 | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
| A. | $\frac{32π}{3}$ | B. | 32π | C. | 64π | D. | $\frac{64π}{3}$ |
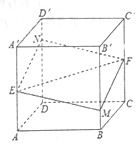 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱是AA′,CC′的中点,过直线EF的平面分别与棱BB′,DD′交于M,N,设BM=x,x∈[0,1],给出以下四种说法:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱是AA′,CC′的中点,过直线EF的平面分别与棱BB′,DD′交于M,N,设BM=x,x∈[0,1],给出以下四种说法:(1)平面MENF⊥平面BDD′B′;
(2)当且仅当x=$\frac{1}{2}$时,四边形MENF的面积最小;
(3)四边形MENF周长L=f(x),x∈[0,1]是单调函数;
(4)四棱锥C′-MENF的体积V=h(x)为常函数,以上说法中正确的为( )
| A. | (2)(3) | B. | (1)(3)(4) | C. | (1)(2)(3) | D. | (1)(2) |
| A. | ?x∉R,x2-x+2>0 | B. | ?x0∈R,x02-x0+2≤0 | ||
| C. | ?x0∈R,$x_0^2-{x_0}+2<0$ | D. | ?x0∉R,$x_0^2-{x_0}+2≤0$ |
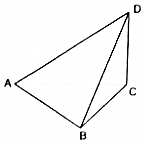 如图所示,在三棱锥D-ABC中,AB=BC=CD=2,AD=2$\sqrt{3}$,∠ABC=90°,平面ACD⊥平面ABC.
如图所示,在三棱锥D-ABC中,AB=BC=CD=2,AD=2$\sqrt{3}$,∠ABC=90°,平面ACD⊥平面ABC.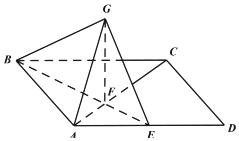 如图,四边形 ABCD是平行四边形,AB=1,AD=2,AC=$\sqrt{3}$,E 是 AD的中点,BE与AC 交于点F,GF⊥平面ABCD.
如图,四边形 ABCD是平行四边形,AB=1,AD=2,AC=$\sqrt{3}$,E 是 AD的中点,BE与AC 交于点F,GF⊥平面ABCD.